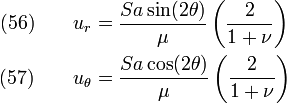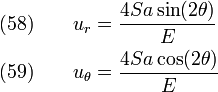Introduction to Elasticity/Plate with hole in shear
< Introduction to ElasticityCircular hole in a shear field
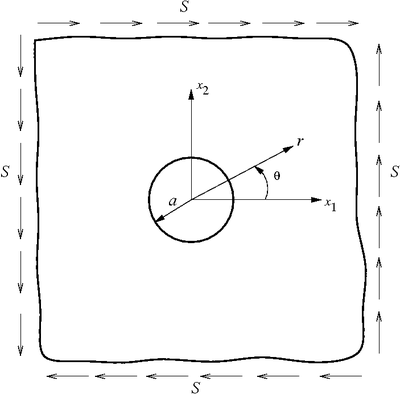 Elastic plate with circular hole under shear |
Given:
- Large plate in pure shear.
- Stress state perturbed by a small hole.
The BCs are
- at

-
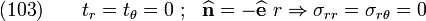
- at
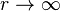
-
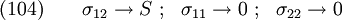
We will solve this problem by superposing a perturbation due to the hole on the unperturbed solution. The effect of the perturbation will decrease with increasing distance from the hole, i.e. the effect will be proportional to 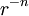 .
.
Unperturbed Solution
Therefore,
Integrating,
Since  is a potential, we can neglect the integration constants (these do not affect the stresses - which are what we are interested in). Hence,
is a potential, we can neglect the integration constants (these do not affect the stresses - which are what we are interested in). Hence,
or,
Note that we have arranged the expression so that it has a form similar to the Fourier series of the previous section.
Perturbed Solution
For this we have to add terms to 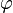 in such a way that
in such a way that
- The unperturbed solution continues to be true as
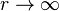 .
. - The terms have the same form as the unperturbed solution,i.e.,
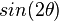 terms.
terms. - The new
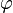 leads to stresses that are proportional to
leads to stresses that are proportional to 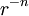 .
.
Recall,
where,
So the appropriate stress function for the perturbation is
or,
Hence, the stress function appropriate for the superposed solution is
We determine 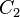 and
and 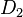 using the boundary conditions at
using the boundary conditions at  .
.
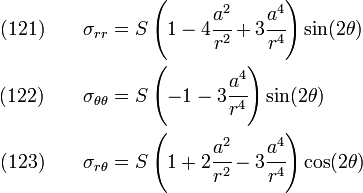
The stresses are
Hence,
or,
Solving,
Back substituting,
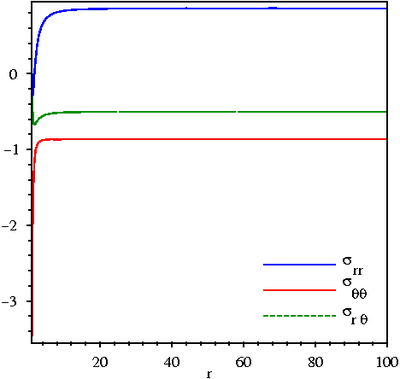 Stresses in elastic plate with circular hole under shear |
Example homework problem
Consider the elastic plate with a hole subject to pure shear.
 Elastic plate with a circular hole under pure shear |
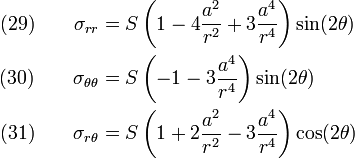
The stresses close to the hole are given by
- Show that the normal and shear traction boundary conditions far from the hole are satisfied by these stresses.
- Calculate the stress concentration factors at the hole, i.e., (
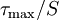 ) (shear) and (
) (shear) and (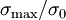 ) (normal).
) (normal). - Calculate the displacement field corresponding to this stress field (for plane stress). Plot the deformed shape of the hole.
Solution
Far from the hole, 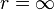 . Therefore,
. Therefore,
To rotate the stresses back to the 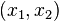 coordinate system, we use the tensor transformation rule
coordinate system, we use the tensor transformation rule
Setting 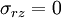 and
and 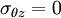 , we get the simplified set of equations
, we get the simplified set of equations
Plugging in equations (32-34) in the above, we have
Hence, the far field stress BCs are satisfied.
The stresses at the hole ( ) are
) are
The maximum (or minimum) hoop stress at the hole is at the locations
where 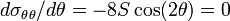 . These locations are
. These locations are 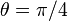 and
and 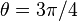 . The value of the hoop stress is
. The value of the hoop stress is
The maximum shear stress is given by
Therefore, the stress concentration factors are
The stress function used to derive the above results was
From Michell's solution, the displacements corresponding to the above stress function are given by
or,
For plane stress, 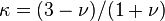 . Hence,
. Hence,
At  ,
,
Now 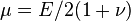 . Hence, we have
. Hence, we have
The deformed shape is shown below
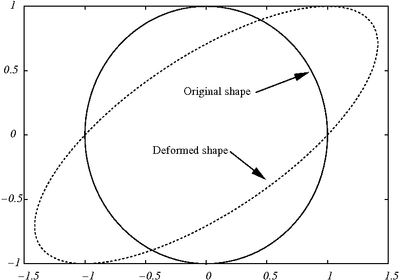 Displacement field near a hole in plate under pure shear |
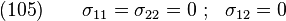
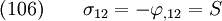
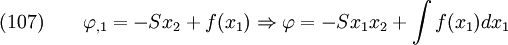
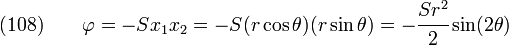
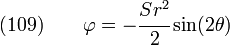
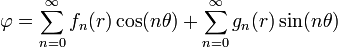
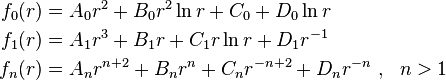

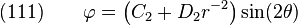
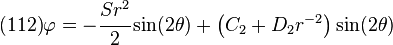
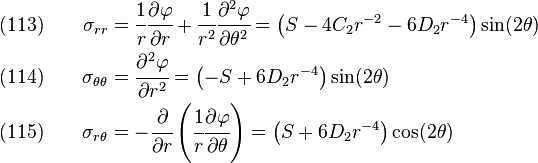
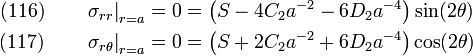
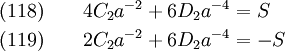
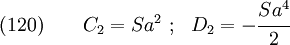
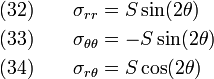
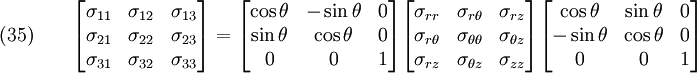
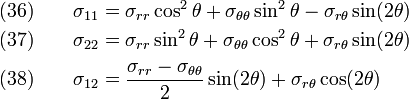
![\begin{align}
\text{(39)} \qquad \sigma_{11} &= -S\left[\sin(2\theta)\cos(2\theta)-\sin(2\theta)\cos(2\theta)
\right] = 0 \\
\text{(40)} \qquad \sigma_{22} &= S\left[\sin(2\theta)\cos(2\theta)-\sin(2\theta)\cos(2\theta)
\right] = 0 \\
\text{(41)} \qquad \sigma_{12} &= S\left[\sin(2\theta)\sin(2\theta)+\cos(2\theta)\cos(2\theta)
\right] = S
\end{align}](../I/m/b4ccb7e6759fe2a76f37667fe424b55f.png)
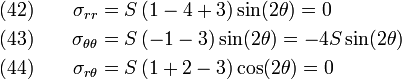
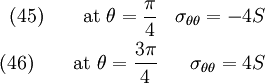
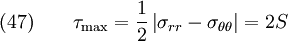
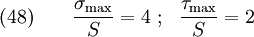
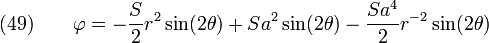
![\begin{align}
\text{(50)} \qquad 2\mu u_r & = -\frac{S}{2}\left[-2r\sin(2\theta)\right]
+Sa^2\left[(\kappa+1)r^{-1}\sin(2\theta)\right]
-\frac{Sa^4}{2}\left[2r^{-3}\sin(2\theta)\right]
\\
\text{(51)} \qquad 2\mu u_{\theta} & = -\frac{S}{2}\left[-2r\cos(2\theta)\right]
+Sa^2\left[(\kappa-1)r^{-1}\cos(2\theta)\right]
-\frac{Sa^4}{2}\left[-2r^{-3}\cos(2\theta)\right]
\end{align}](../I/m/9db6787b7f26da2c252a3504d4653c4b.png)
![\begin{align}
\text{(52)} \qquad u_r & = \frac{Sr\sin(2\theta)}{2\mu}\left[
1 + (\kappa+1)\frac{a^2}{r^2} - \frac{a^4}{r^4}\right]
\\
\text{(53)} \qquad u_{\theta} & = \frac{Sr\cos(2\theta)}{2\mu}\left[
1 + (\kappa-1)\frac{a^2}{r^2} + \frac{a^4}{r^4}\right]
\end{align}](../I/m/525b1584d44f782cdbe81ab13f64faad.png)
![\begin{align}
\text{(54)} \qquad u_r & = \frac{Sr\sin(2\theta)}{2\mu}\left[
1 + \left(\frac{4}{1+\nu}\right)\frac{a^2}{r^2}
- \frac{a^4}{r^4}\right]
\\
\text{(55)} \qquad u_{\theta} & = \frac{Sr\cos(2\theta)}{2\mu}\left[
1 + 2\left(\frac{1-\nu}{1+\nu}\right)\frac{a^2}{r^2}
+ \frac{a^4}{r^4}\right]
\end{align}](../I/m/151b970c9d6915ab8c92a63d73c9e460.png)