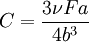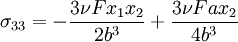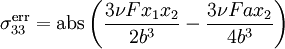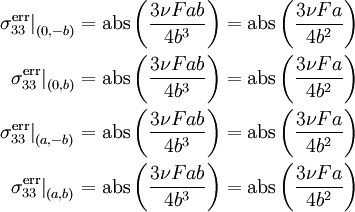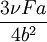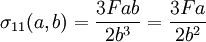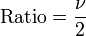Introduction to Elasticity/Plane strain example 1
< Introduction to ElasticityExample 1
Given:
The plane strain solution for the stresses in a rectangular block
with 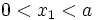 ,
, 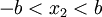 , and
, and 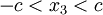 with a given loading is
with a given loading is
Find:
- Find the tractions on the surfaces of the block and illustrate the results on a sketch of the block.
- We wish to use this solution to solve the corresponding problem in which the surfaces
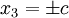 are traction-free. Determine an approximate corrective solution for this problem by offloading the unwanted force and moment results using elementary bending theory.
are traction-free. Determine an approximate corrective solution for this problem by offloading the unwanted force and moment results using elementary bending theory. - Find the maximum error in the stress
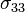 in the corrected solution and compare it with the maximum tensile stress in the plane strain solution.
in the corrected solution and compare it with the maximum tensile stress in the plane strain solution.
Solution
The tractions acting on the block are:
Plugging in the expressions for stress,
These tractions are illustrated in the following figure
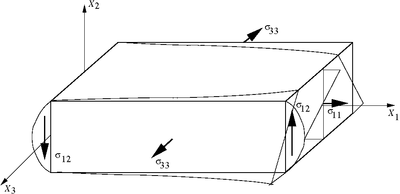 Tractions on the beam |
To unload the tractions on the faces  , we have to superpose the solution to a problem with equal and opposite tractions and moments. In order to use elementary bending theory, we have set up a problem with simple boundary conditions.
, we have to superpose the solution to a problem with equal and opposite tractions and moments. In order to use elementary bending theory, we have set up a problem with simple boundary conditions.
Let us first consider the force distribution required for the superposed problem. Since the loading is antisymmetric at  , there is no net force is the
, there is no net force is the  direction. Similarly, there is no net moment about the
direction. Similarly, there is no net moment about the 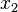 axis.
axis.
However, there is a net moment about the  axis. Hence, the problem to be superposed should have a bending stress distribution
axis. Hence, the problem to be superposed should have a bending stress distribution 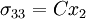 , where
, where 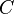 is a constant that is chosen so as to make the total bending moment (original problem + superposed problem) equal to zero. (Note: Think of a beam in the
is a constant that is chosen so as to make the total bending moment (original problem + superposed problem) equal to zero. (Note: Think of a beam in the 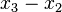 plane subjected to bending moments at the ends.)
plane subjected to bending moments at the ends.)
The total stress for the corrected problem is
The bending moment for a cross-section of the beam in the
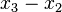 plane about the
plane about the  axis is
axis is 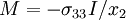 , where
, where
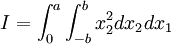 .
.
Since 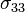 varies with
varies with
 , the total bending moment for the beam is given by
, the total bending moment for the beam is given by
Setting the bending moment to zero, we have
Therefore, the corrected solution is
Ideally, for a problem with zero tractions on 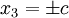 , we should have
, we should have 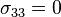 . Therefore, the error in our solution is
. Therefore, the error in our solution is
The error is maximum at 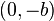 ,
, 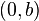 ,
, 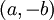 , and
, and 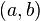 . Thus,
. Thus,
The maximum error is
The maximum tensile stress is
Therefore, the ratio of the maximum error in 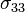 to the maximum
tensile stress is
to the maximum
tensile stress is
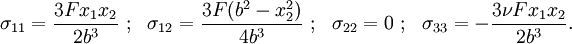
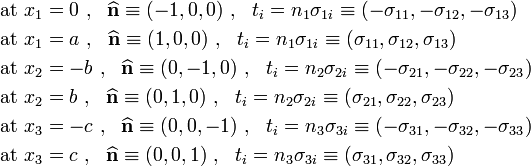
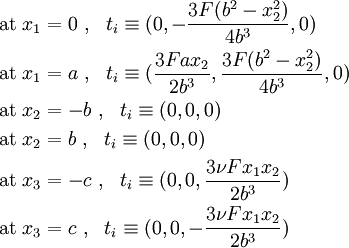
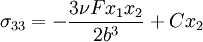
![\begin{align}
M & = \int_0^a \int_{-b}^b \left(\frac{-\sigma_{33}}{x_2}\right)
x_2^2 dx_2 dx_1 \\
& = \int_0^a \int_{-b}^b \left(\frac{3 \nu F x_1 x_2}{2 b^3} - C x_2 \right)
x_2 dx_2 dx_1 \\
& = \int_0^a \left[\frac{3\nu F x_1 x_2^3}{6 b^3} - \frac{C x_2^3}{3}
\right]_{-b}^b dx_1 \\
& = \int_0^a \left[\frac{\nu F x_1 b^3}{b^3} - \frac{2C b^3}{3}
\right] dx_1 \\
& = \left[\frac{\nu F x_1^2 b^3}{2b^3} - \frac{2C x_1 b^3}{3}
\right]_0^a \\
& = \frac{\nu F a^2 b^3}{2b^3} - \frac{2C a b^3}{3}
\end{align}](../I/m/0cb74beb96baf192de85f57bdc764c55.png)