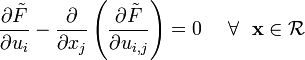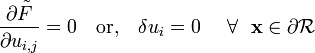Introduction to Elasticity/Minimizing a functional
< Introduction to ElasticityMinimizing a Functional in 1-D
In 1-D, the minimization problem can be stated as
Find  such that
such that
is a minimum.
We have seen that the minimization problem can be reduced down to the solution of an Euler equation
with the associated boundary conditions
or,
Minimizing a Functional in 3-D
In 3-D, the equivalent minimization problem can be stated as
Find  such that
such that
is a minimum.
We would like to find the Euler equation for this problem and the associated boundary conditions required to minimize 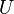 .
.
Let us define all our quantities with respect to an orthonormal basis 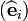 .
.
Then,
and
Taking the first variation of 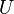 , we get
, we get
All the nine components of 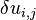 are not independent. Why ?
are not independent. Why ?
The variation of the functional 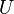 needs to be expressed
entirely in terms of
needs to be expressed
entirely in terms of 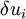 . We do this using the 3-D equivalent of integration by parts - the divergence theorem.
. We do this using the 3-D equivalent of integration by parts - the divergence theorem.
Thus,
Substituting in the expression for 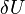 , we have,
, we have,
For 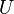 to be minimum, a necessary condition is that
to be minimum, a necessary condition is that 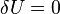 for all variations
for all variations 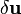 .
.
Therefore, the Euler equation for this problem is
and the associated boundary conditions are
![U[u(x)] = \int_{x_0}^{x_1} F(x,u,u^{'}) dx](../I/m/b88fe2225ff56df8761da790dc3f45ea.png)
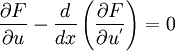
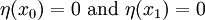
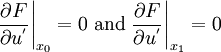
![U[\mathbf{u}(\mathbf{x})] = \int_{\mathcal{R}} F(\mathbf{x},\mathbf{u},\boldsymbol{\nabla}\mathbf{u})~dV](../I/m/a867e78d5b15eb15662a2bfbe5720838.png)
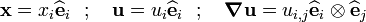
![U[\mathbf{u}(\mathbf{x})] = \int_{\mathcal{R}} \tilde{F}(x_i, u_i, u_{i,j})~dV](../I/m/f2cb78d9d20633d171414a332f745f53.png)
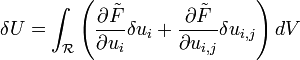
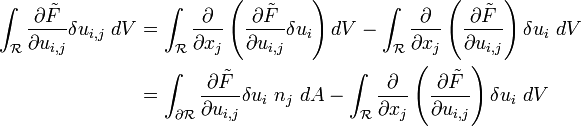
![\begin{align}
\delta U &= \int_{\mathcal{R}} \frac{\partial \tilde{F}}{\partial u_i} \delta u_i~dV +
\int_{\partial\mathcal{R}} \frac{\partial \tilde{F}}{\partial u_{i,j}} \delta u_i~n_j~dA -
\int_{\mathcal{R}} \frac{\partial }{\partial x_j} \left(\frac{\partial \tilde{F}}{\partial u_{i,j}} \right)
\delta u_i~ dV \\
&= \int_{\mathcal{R}}\left[\frac{\partial \tilde{F}}{\partial u_i} -
\frac{\partial }{\partial x_j}\left(\frac{\partial \tilde{F}}{\partial u_{i,j}} \right)\right]
\delta u_i~ dV +
\int_{\partial\mathcal{R}} \frac{\partial \tilde{F} }{\partial u_{i,j}} \delta u_i~n_j~dA
\end{align}](../I/m/2923fa0ead48627c6b97e0c89e7ca76b.png)