Introduction to Elasticity/Kinematics example 3

Example 3

Given:

Unit square $(X_1,X_2) \in [0,1]$ with displacement fields :

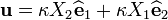$\mathbf{u} = \kappa X_2 \widehat{\mathbf{e}}_{1} + \kappa X_1 \widehat{\mathbf{e}}_{2}$ .
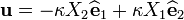$\mathbf{u} = -\kappa X_2 \widehat{\mathbf{e}}_{1} + \kappa X_1 \widehat{\mathbf{e}}_{2}$ .
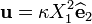$\mathbf{u} = \kappa X_1^2 \widehat{\mathbf{e}}_{2}$ .

Sketch: Deformed configuration in 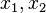$x_1,x_2$ plane.

Solution

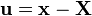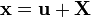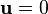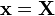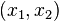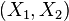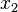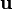The displacement $\mathbf{u} = \mathbf{x} - \mathbf{X}$ . Hence, $\mathbf{x} = \mathbf{u} + \mathbf{X}$ . In the reference configuration, $\mathbf{u} = 0$ and $\mathbf{x} = \mathbf{X}$ . Hence, in the $(x_1, x_2)$ plane, the initial square is the same shape as the unit square in the $(X_1, X_2)$ plane. We can use Maple to find out the values of $x_1$ and $x_2$ after the deformation $\mathbf{u}$ .


  with(linalg):</code>
  X := array(1..3): x := array(1..3): u = array(1..3):
  e1 := array(1..3,[1,0,0]): 
  e2 := array(1..3,[0,1,0]): e3 = array(1..3,[0,0,1]):
  ua := evalm(k*X[2]*e1 + k*X[1]*e2):
  ub := evalm(-k*X[2]*e1 + k*X[1]*e2);
  uc := evalm(k*X[1]^2*e2);

\mathit{ua} := \left[ k{X_{2}}, k{X_{1}}, 0 \right]

\mathit{ub} := \left[ - k{X_{2}}, k{X_{1}}, 0 \right]

\mathit{uc} := \left[ 0, k{X_{1}}^{2}, 0 \right]


  xa := evalm(ua + X);
  xb := evalm(ub + X);
  xc := evalm(uc + X);</code>

\mathit{xa} := \left[ k{X_{2}} + {X_{1}}, k{X_{1}} + {X_{2}}, {X_{3}} \right]

\mathit{xb} := \left[ - k{X_{2}} + {X_{1}}, k{X_{1}} + {X_{2}}, {X_{3}} \right]

\mathit{xc} := \left[ {X_{1}}, k{X_{1}}^{2} + {X_{2}}, {X_{3}} \right]

Plots of the deformed body are shown below

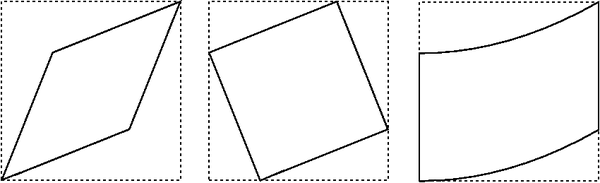Deformed shapes

This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.