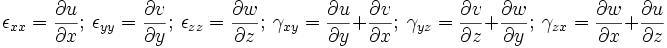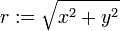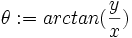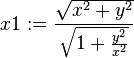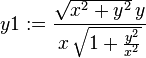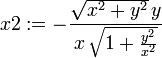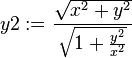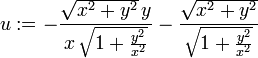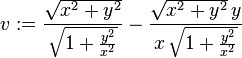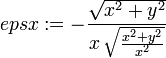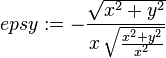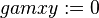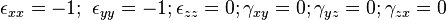Introduction to Elasticity/Kinematics example 1

< Introduction to Elasticity

Example 1

Take a unit cube of material. Rotate it 90 degrees in the clockwise direction around the z-axis. Calculate the strains. Discuss your results - their accuracy and the reasons for your conclusions.

Solution

The strains are related to displacements by

\epsilon_{xx} = \frac{\partial u}{\partial x};~ \epsilon_{yy} = \frac{\partial v}{\partial y};~ \epsilon_{zz} = \frac{\partial w}{\partial z};~ \gamma_{xy} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x};~ \gamma_{yz} = \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y};~ \gamma_{zx} = \frac{\partial w}{\partial x} + \frac{\partial u}{\partial z}

Let us consider rotation about the center of the cube. Since the problem concerns a pure rotation, a cylindrical co-ordinate system is appropriate. This problem also provides us a easy way of trying out Maple. Here are the steps that you can follow to find the strains at a point in the cube.


r := sqrt(x^2+y^2);

r := \sqrt{x^{2} + y^{2}}


theta := arctan(y/x);

\theta := arctan(\frac{y}{x})


x1 := r*cos(theta);

x1 := \frac{\sqrt{x^2 + y^2}}{\sqrt{1 + \frac{y^2}{x^2}}}


y1 := r*sin(theta);

y1 := \frac{\sqrt{x^2 + y^2}\,y}{x\,\sqrt{1 + \frac{y^2}{x^2}}}


x2 := r*cos(theta+Pi/2);

x2 := -\frac{\sqrt{x^2 + y^2}\,y}{x\,\sqrt{1 + \frac{y^2}{x^2}}}


y2 := r*sin(theta+Pi/2);

y2 := \frac{\sqrt{x^2 + y^2}}{\sqrt{1 + \frac {y^2}{x^2}}}


u := x2 - x1;

u := -\frac{\sqrt{x^2 + y^2}\,y}{x\,\sqrt{1 + \frac {y^2}{x^2}}} -\frac{\sqrt{x^2 + y^2}}{\sqrt{1 + \frac {y^2}{x^2}}}


v := y2 - y1;

v := \frac{\sqrt{x^2 + y^2}}{\sqrt{1 + \frac {y^2}{x^2} }} - \frac{\sqrt{x^2 + y^2}\,y}{x\,\sqrt{1 + \frac {y^2}{x^2}}}


epsx := simplify(diff(u,x));

epsx := -\frac{\sqrt{x^2 + y^2}}{x\,\sqrt{\frac{x^2 + y^2}{x^2}}}


epsy := simplify(diff(v,y));

epsy := -\frac{\sqrt{x^2 + y^2}}{x\,\sqrt{\frac{x^2 + y^2}{x^2}}}


gamxy := simplify(diff(u,y) + diff(v,x));

gamxy := 0

From the above Maple calculation, and noting that there is no motion in the 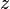z direction, the strains in the cube are

\epsilon_{xx} = -1;~\epsilon_{yy} = -1; \epsilon_{zz} = 0; \gamma_{xy} = 0; \gamma_{yz} = 0; \gamma_{zx} = 0

A pure rigid body rotation should not result in any non-zero strains.

Therefore, the measure of strain we have used is not appropriate for large rigid body motions.

This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.