Introduction to Elasticity/Hu-Washizu principle

Hu-Washizu Variational Principle

In this case, the admissible states are not required to meet any of the field equations or boundary conditions.

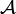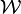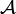Let $\mathcal{A}$ denote the set of all admissible states and let $\mathcal{W}$ be a functional on $\mathcal{A}$ defined by

{\mathcal W}[s] = \int_{\mathcal{B}} U(\boldsymbol{\varepsilon}) - \int_{\mathcal{B}} \boldsymbol{\sigma}:\boldsymbol{\varepsilon}~dV - \int_{\mathcal{B}} (\boldsymbol{\nabla}\bullet{\boldsymbol{\sigma}} + \mathbf{f})\bullet\mathbf{u}~dV + \int_{\partial{\mathcal{B}}^{u}} \mathbf{t}\bullet\widehat{\mathbf{u}}~dA + \int_{\partial{\mathcal{B}}^{t}} (\mathbf{t}-\widehat{\mathbf{t}})\bullet\mathbf{u}~dA

for every $s = [\mathbf{u},\boldsymbol{\varepsilon},\boldsymbol{\sigma}] \in \mathcal{A}$ .

Then,

\delta {\mathcal W}[s] = 0

at an admissible state $s$ if and only if $s$ is a solution of the mixed problem.

This article is issued from Wikiversity - version of the Sunday, September 02, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.