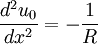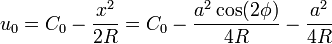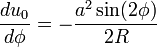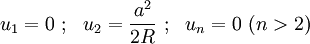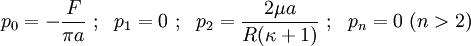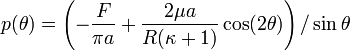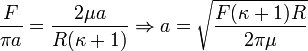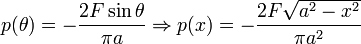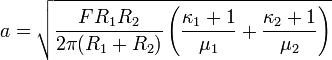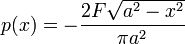Introduction to Elasticity/Hertz contact

< Introduction to Elasticity

The Hertz Problem: Rigid Cylindrical Punch

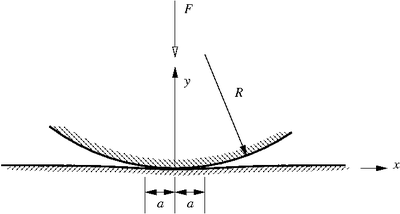Hertz indentation

The contact length 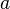$a$ depends on the load $F\,$ .
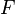There is no singularity at $x = \pm a$ .
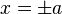The radius of the cylinder ( 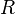$R\,$ ) is large.

We have,

\frac{d^2 u_0}{dx^2} = -\frac{1}{R}

Hence,

u_0 = C_0 - \frac{x^2}{2R} = C_0 - \frac{a^2\cos(2\phi)}{4R}-\frac{a^2}{4R}

and

\frac{d u_0}{d\phi} = -\frac{a^2\sin(2\phi)}{2R}

Therefore,

u_1 = 0 ~;~~ u_2 = \frac{a^2}{2R} ~;~~ u_n = 0 ~(n > 2)

and

p_0 = -\frac{F}{\pi a} ~;~~ p_1 = 0 ~;~~ p_2 = \frac{2\mu a}{R(\kappa+1)} ~;~~ p_n = 0 ~(n > 2)

Plug back into the expression for 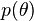$p(\theta)$ to get

p(\theta) = \left(-\frac{F}{\pi a} + \frac{2\mu a}{R(\kappa+1)}\cos(2\theta) \right)/\sin\theta

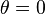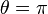This expression is singular at $\theta=0$ and $\theta=\pi$ , unless we choose

\frac{F}{\pi a} = \frac{2\mu a}{R(\kappa+1)} \Rightarrow a = \sqrt{\frac{F(\kappa+1)R}{2\pi\mu}}

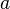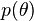Plugging $a$ into the equation for $p(\theta)$ ,

p(\theta) = -\frac{2F\sin\theta}{\pi a} \Rightarrow p(x) = -\frac{2F\sqrt{a^2-x^2}}{\pi a^2}

Two deformable cylinders

If instead of the half-plane we have an cylinder; and instead of the rigid cylinder we have a deformable cylinder, then a similar approach can be used to obtain the contact length 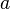$a\,$

a = \sqrt{\frac{FR_1R_2}{2\pi(R_1+R_2)}\left( \frac{\kappa_1+1}{\mu_1} + \frac{\kappa_2+1}{\mu_2}\right)}

and the force distribution 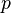$p$

p(x) = -\frac{2F\sqrt{a^2-x^2}}{\pi a^2}

This article is issued from Wikiversity - version of the Wednesday, August 08, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.