Introduction to Elasticity/Hellinger-Reissner principle

Hellinger-Prange-Reissner Variational Principle

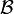In this case, we assume that the elasticity field is invertible and $s$ is smooth on $\mathcal{B}$ . We also assume that 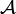$\mathcal{A}$ is the set of all admissible states that satisfy the strain-displacement relations.

Let 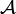$\mathcal{A}$ denote the set of all admissible states and let 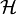$\mathcal{H}$ be a functional on 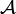$\mathcal{A}$ defined by

{\mathcal H}[s] = \int_{\mathcal{B}} U^c(\boldsymbol{\sigma}) - \int_{\mathcal{B}} \boldsymbol{\sigma}:\boldsymbol{\varepsilon}~dV - \int_{\mathcal{B}} \mathbf{f}\bullet\mathbf{u}~dV + \int_{\partial{\mathcal{B}}^{u}} \mathbf{t}\bullet(\mathbf{u}-\widehat{\mathbf{u}})~dA + \int_{\partial{\mathcal{B}}^{t}} \widehat{\mathbf{t}}\bullet\mathbf{u}~dA

for every $s = [\mathbf{u},\boldsymbol{\varepsilon},\boldsymbol{\sigma}] \in \mathcal{A}$ .

Then,

\delta {\mathcal H}[s] = 0

at an admissible state 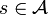$s\in\mathcal{A}$ if and only if $s$ is a solution of the mixed problem.

This article is issued from Wikiversity - version of the Wednesday, November 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.