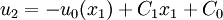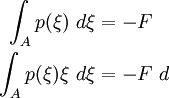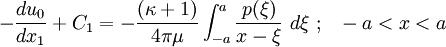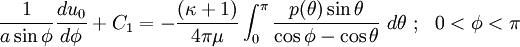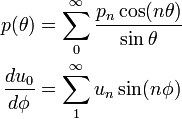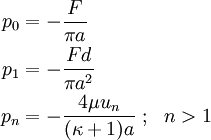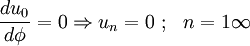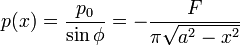Introduction to Elasticity/Flat punch indentation
< Introduction to ElasticityIndentation due to a Frictionless Rigid Flat Punch
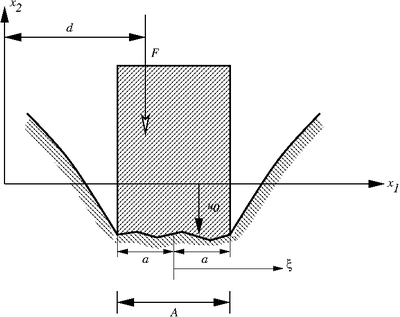 Indentation by a plat rigid punch |
- Start with uneven surface profile
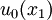 .
. - Unsymmetric load
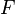 , but sufficient for complete contact over the area
, but sufficient for complete contact over the area 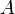 .
.
Displacement in  direction is
direction is
where 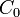 is a rigid body translation and
is a rigid body translation and 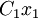 is a rigid body rotation.
is a rigid body rotation.
Rigid body motions can be determined using a statically equivalent set of forces and moments
The displacement gradient is
Integral is a Cauchy Singular Integral that appears often and very naturally when the problem is solved using complex variable methods.
Note that the only thing we are interested in is the distribution
of contact forces 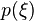 .If we change the variables so that
.If we change the variables so that
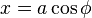 and
and 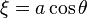 , then
, then
If we write 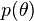 and
and 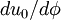 as
as
and do some algebra, we get
Flat Punch with Symmetric Load: 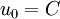
In this case,
Also, 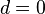 (origin at the center of
(origin at the center of 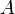 ), hence
), hence 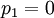 . Therefore,
. Therefore,
At 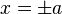 , the load is infinite, i.e. there is a singularity.
, the load is infinite, i.e. there is a singularity.
This article is issued from Wikiversity - version of the Wednesday, August 08, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.