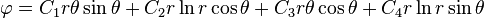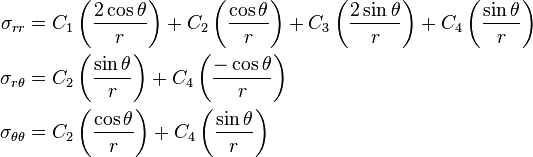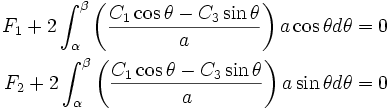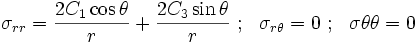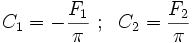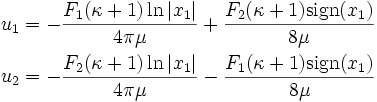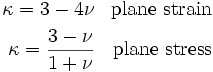Introduction to Elasticity/Flamant solution
< Introduction to ElasticityThe Flamant Solution
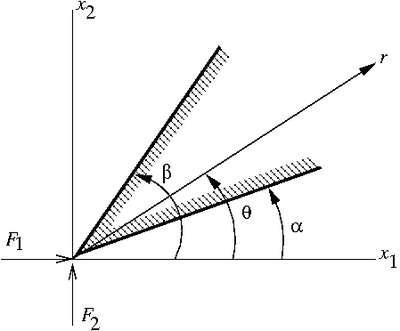 Elastic wedge loaded by two forces at the tip |
- This problem is also self-similar (no inherent length scale).
- All quantities can be expressed in the separated-variable form
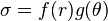 .
. - The stresses vary as
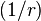 (the area of action of the force decreases with increasing
(the area of action of the force decreases with increasing  ). How about a conical wedge ?
). How about a conical wedge ?
From Michell's solution, pick terms containing 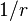 in the stresses.
Then,
in the stresses.
Then,
Therefore, from Tables,
From traction BCs, 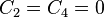 .
From equilibrium,
.
From equilibrium,
After algebra,
Special Case : 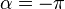 ,
, 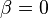
The displacements are
where
and
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.