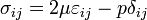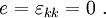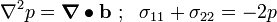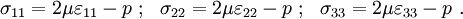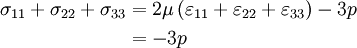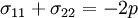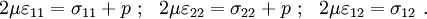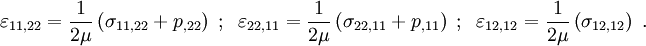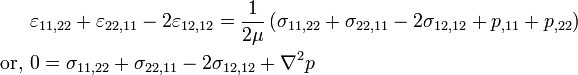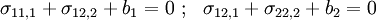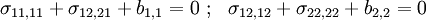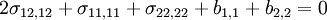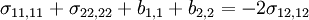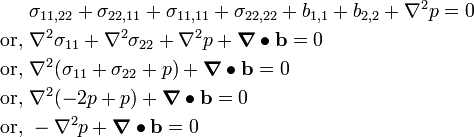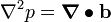Introduction to Elasticity/Equilibrium example 3
< Introduction to ElasticityExample 3
Given:
If a material is incompressible (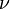 = 0.5), a state of hydrostatic stress (
= 0.5), a state of hydrostatic stress (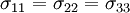 ) produces no strain. The corresponding stress-strain relation can be written as
) produces no strain. The corresponding stress-strain relation can be written as
where 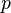 is an unknown hydrostatic pressure which will generally vary with position. Also, the condition of incompressibility requires that the dilatation
is an unknown hydrostatic pressure which will generally vary with position. Also, the condition of incompressibility requires that the dilatation
Show:
Show that the stress components and the hydrostatic pressure 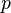 must satisfy the equations
must satisfy the equations
where 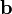 is the body force.
is the body force.
Solution
We have, 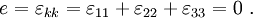 Also,
Also,
Therefore,
Since 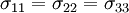 , the above relation
gives
, the above relation
gives 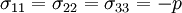 .
Therefore,
.
Therefore,
The strain-stress relations are
Differentiating the strains so that they correspond to the compatibilityrelation is two-dimensions, we have
In terms of the compatibility equation,
From the two-dimensional equilibrium equations,
Therefore, differentiating w.r.t 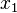 and
and 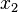 respectively,
respectively,
Adding,
Hence,
Substituting back into the compatibility equation,
Hence,