Introduction to Elasticity/Equilibrium example 2
< Introduction to ElasticityExample 2
Given: The displacement equation of equilibrium for an isotropic inhomogeneous linear elastic material can be written as
where
and 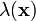 and
and 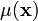 are the Lamé moduli.
are the Lamé moduli.
Show:
Show that the displacement equation of equilibrium can be expressed as
Solution
The skew part of the tensor 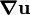 does not affect the stress because it leads to a rigid displacement field. Therefore, the displacement equation of equilibrium may be written as
does not affect the stress because it leads to a rigid displacement field. Therefore, the displacement equation of equilibrium may be written as
where
In index notataion,
and
Therefore,
Now,
Hence,
Taking the divergence,
Recall that
Therefore,
Hence,
Therefore, the displacement equation of equilibrium can be expressed as required, i.e,
This article is issued from Wikiversity - version of the Saturday, February 13, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
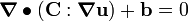
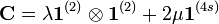
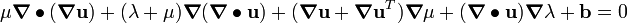
![\boldsymbol{\nabla} \bullet \left[\mathbf{C} : \text{symm}(\boldsymbol{\nabla}\mathbf{u})\right] + \mathbf{b} = 0](../I/m/1702f5006acb0d0f47df760ebf9c3440.png)
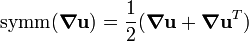
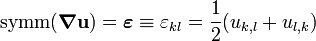
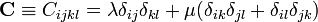
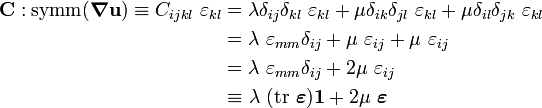
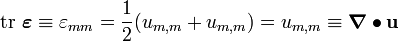
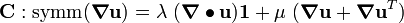
![\begin{align}
\boldsymbol{\nabla}\bullet{\left[\mathbf{C} : \text{symm}(\boldsymbol{\nabla}\mathbf{u})\right]} & =
\boldsymbol{\nabla}\bullet{\left[\lambda~(\boldsymbol{\nabla}\bullet\mathbf{u})\mathbf{1} + \mu~(\boldsymbol{\nabla}\mathbf{u} + \boldsymbol{\nabla}\mathbf{u}^T)\right]} \\
& = \boldsymbol{\nabla}\bullet{\left[\lambda~(\boldsymbol{\nabla}
\bullet\mathbf{u})\mathbf{1}\right]} +
\boldsymbol{\nabla}\bullet{\left(\mu~\boldsymbol{\nabla}\mathbf{u}\right)} +
\boldsymbol{\nabla}\bullet{\left(\mu~\boldsymbol{\nabla}\mathbf{u}^T\right)}
\end{align}](../I/m/cdc63c5bd5a4a8fe1f8e6281de6f83da.png)
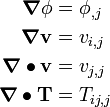
![\begin{align}
\boldsymbol{\nabla}\bullet{\left[\lambda~(\boldsymbol{\nabla}
\bullet\mathbf{u})\mathbf{1}\right]} &
\equiv \left(\lambda~u_{k,k}\delta_{ij}\right)_{,j} \\
& = \lambda_{,i}~u_{k,k} + \lambda~u_{k,ki} \\
& \equiv \boldsymbol{\nabla}{\lambda}(\boldsymbol{\nabla}\bullet\mathbf{u}) + \lambda\boldsymbol{\nabla}{(\boldsymbol{\nabla}\bullet\mathbf{u})}
\end{align}](../I/m/8200d709405f2b7d5e0713561db58410.png)
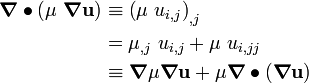
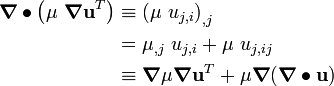
![\begin{align}
\boldsymbol{\nabla}\bullet{\left[\mathbf{C} : \text{symm}(\boldsymbol{\nabla}\mathbf{u})\right]}
& = \boldsymbol{\nabla}{\lambda}(\boldsymbol{\nabla}
\bullet\mathbf{u}) + \lambda\boldsymbol{\nabla}{(\boldsymbol{\nabla}\bullet\mathbf{u})} +
\boldsymbol{\nabla}{\mu} \boldsymbol{\nabla}\mathbf{u} + \mu\boldsymbol{\nabla}\bullet{(\boldsymbol{\nabla}\mathbf{u})} +
\boldsymbol{\nabla}{\mu} \boldsymbol{\nabla}\mathbf{u}^{T} + \mu\boldsymbol{\nabla}{(\boldsymbol{\nabla}\bullet\mathbf{u})} \\
& = \mu\boldsymbol{\nabla}\bullet{(\boldsymbol{\nabla}\mathbf{u})} + (\lambda+\mu)\boldsymbol{\nabla}{(\boldsymbol{\nabla}\bullet\mathbf{u})} +
\boldsymbol{\nabla}{\mu}\left(\boldsymbol{\nabla}\mathbf{u} + \boldsymbol{\nabla}\mathbf{u}^{T}\right) +
\boldsymbol{\nabla}{\lambda}(\boldsymbol{\nabla}\bullet \mathbf{u})
\end{align}](../I/m/d5f96dbba6b7bba7a844b5ada801783a.png)