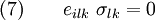Introduction to Elasticity/Equilibrium example 1
< Introduction to ElasticityExample 1
Given:
Euler's second law for the conservation of angular momentum
The divergence theorem
The equilibrium equation (Cauchy's first law)
Show:
Solution
Let us first look at the first term of equation~(1) and apply the divergence theorem (2). Thus,
Plugging this back into equation~(1) gives
Therefore, bringing all terms to the left hand side,
Using the equilibrium equations~(3), equation~(5) reduces to
Since this holds for any 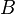 , we have
, we have
If you work this expression out, you will see that  .
Hence, the stress tensor is symmetric.
.
Hence, the stress tensor is symmetric.
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
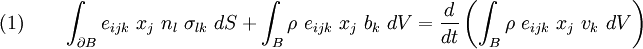
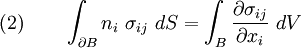
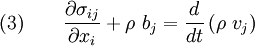
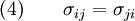
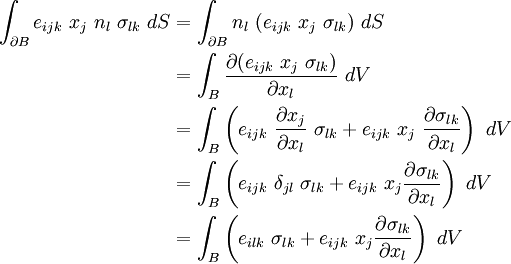
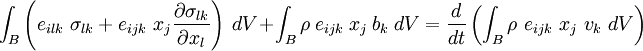
![\text{(5)} \qquad
\int_{B} \left[e_{ilk}~\sigma_{lk} +
e_{ijk}~x_j\left(\frac{\partial\sigma_{lk}}{\partial x_l}
+ \rho~b_k - \frac{d}{dt}\left(\rho~v_k\right)\right)\right]~dV = 0](../I/m/d6ed01a09efb6e7cde4a860b83d4d86a.png)