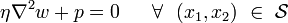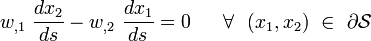Introduction to Elasticity/Energy methods example 2
< Introduction to ElasticityExample 2
Given:
The potential energy functional for a membrane stretched over a simply connected region  of the
of the  plane can be expressed as
plane can be expressed as
where 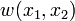 is the deflection of the membrane,
is the deflection of the membrane, 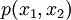 is the prescribed transverse pressure distribution, and
is the prescribed transverse pressure distribution, and 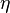 is the membrane stiffness.
is the membrane stiffness.
Find:
- The governing differential equation (Euler equation) for
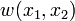 on
on 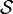 .
. - The permissible boundary conditions at the boundary
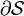 of
of 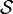 .
.
Solution
The principle of minimum potential energy requires that the functional 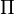 be stationary for the actual displacement field
be stationary for the actual displacement field 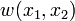 . Taking the first variation of
. Taking the first variation of 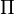 , we get
, we get
or,
Now,
Therefore,
Plugging into the expression for 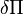 ,
,
or,
Now, the Green-Riemann theorem states that
Therefore,
or,
where  is the arc length around
is the arc length around 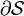 .
.
The potential energy function is rendered stationary if 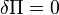 . Since
. Since 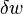 is arbitrary, the condition of stationarity is satisfied only if the governing differential equation for
is arbitrary, the condition of stationarity is satisfied only if the governing differential equation for 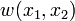 on
on  is
is
The associated boundary conditions are
![\Pi[w(x_1,x_2)] = \frac{1}{2}\int_{\mathcal{S}} \eta\left[(w_{,1})^2 + (w_{,2})^2\right]
~dA - \int_{\mathcal S} pw~dA](../I/m/9cbda4d1b5fa39a3ea37448e42f2cf7f.png)
![\delta\Pi = \frac{\eta}{2}\int_{\mathcal S} \left[(2 w_{,1})\delta w_{,1} +
(2 w_{,2})\delta w_{,2}\right] ~dA - \int_{\mathcal S} p~\delta w~dA](../I/m/046c28e2bb74a7e0e588631a3aefbd0a.png)
![\delta\Pi = \eta\int_{\mathcal S} \left[w_{,1}~\delta w_{,1} +
w_{,2}~\delta w_{,2}\right] ~dA - \int_{\mathcal S} p~\delta w~dA](../I/m/faa59c96eb0206c7581076b8b1b15297.png)
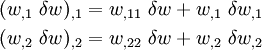
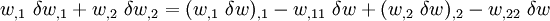
![\delta\Pi = \eta\int_{\mathcal S}
\left[(w_{,1}~\delta w)_{,1} + (w_{,2}~\delta w)_{,2} -
(w_{,11} + w_{,22})~\delta w\right]~dA
- \int_{\mathcal S} p~\delta w~dA](../I/m/5fe2c53956e5110f533837a7c90416a4.png)
![\delta\Pi = \eta\int_{\mathcal S}
\left[(w_{,1}~\delta w)_{,1} + (w_{,2}~\delta w)_{,2}\right]~dA -
\eta\int_{\mathcal S} \nabla^2{w}~\delta w~dA
- \int_{\mathcal S} p~\delta w~dA](../I/m/3013c8d5b01db144657fda348f676c1f.png)
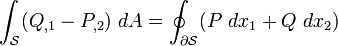
![\delta\Pi = \eta\oint_{\partial{\mathcal S}}
\left[(w_{,1}~\delta w)~dx_2 - (w_{,2}~\delta w)~dx_1\right] -
\int_{\mathcal S}\left[\eta\nabla^2{w}+p\right]~\delta w~dA](../I/m/f1718d6ca23eb17271a80836e71997f4.png)
![\delta\Pi = \eta\oint_{\partial{\mathcal S}}
\left[w_{,1}~\frac{dx_2}{ds} - w_{,2}~\frac{dx_1}{ds}\right]\delta w~ds -
\int_{\mathcal S}\left[\eta\nabla^2{w}+p\right]~\delta w~dA](../I/m/20b2808d0abf37aa804bd806171543a2.png)