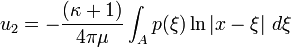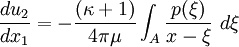Introduction to Elasticity/Distributed force on half plane

Distributed Force on a Half-Plane

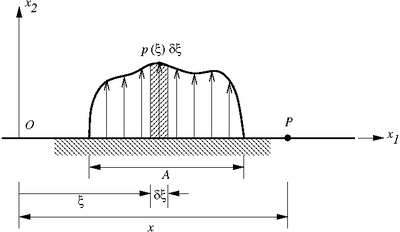Distributed force on a half plane

Applied load is 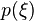$p(\xi)\,$ per unit length in the $x_2\,$ direction.
We already know the stresses and displacements due to a concentrated force. The stresses and displacements due to the distributed load can be found by superposition.
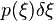The Flamant solution is used as a Green's function, i.e., the distributed load is taken as the limit of a set of point loads of magnitude $p(\xi)\delta\xi\,$ .

At the point 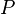$P\,$

u_2 = - \frac{(\kappa+1)}{4\pi\mu} \int_A p(\xi)\ln|x - \xi|~d\xi

As 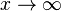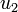$x \rightarrow \infty\,$ , $u_2\,$ is unbounded. However, if we are interested in regions far from 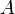$A\,$ , we can apply the distributed force as a statically equivalent concentrated force and get displacements using the concentrated force solution.

The avoid the above issue, contact problems are often formulated in terms of the displacement gradient

\frac{du_2}{dx_1} = - \frac{(\kappa+1)}{4\pi\mu} \int_A \frac{p(\xi)}{x - \xi}~d\xi

If the point 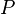$P\,$ is inside 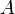$A\,$ , then the integral is taken to be the sum of the integrals to the left and right of $P\,$ .

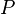This article is issued from Wikiversity - version of the Wednesday, August 08, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.