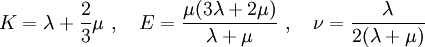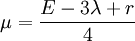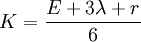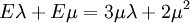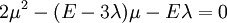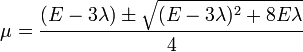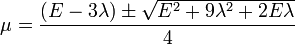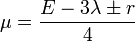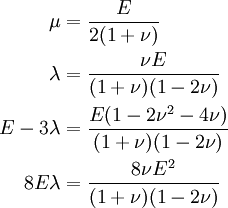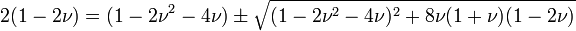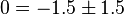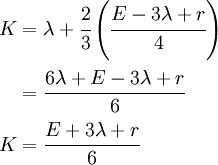Introduction to Elasticity/Constitutive example 6
< Introduction to ElasticityExample 6
Given:
For an isotropic material
Verify:
where 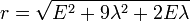 .
.
Solution
From the second equation that has been given
or,
Therefore,
or,
or,
To find out whether the plus or the minus sign should be placed before  in the above equation, we put everything in terms of
in the above equation, we put everything in terms of 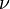 and
and  . Thus,
. Thus,
Plugging these into the equation for 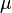 , multiplying both sides by
, multiplying both sides by 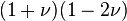 and dividing by
and dividing by  , we get
, we get
The limiting value of 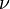 is 0.5. Plugging this value into the above equation, we get,
is 0.5. Plugging this value into the above equation, we get,
The above can be true only if the sign is positive. Therefore, the correct relation is
Plugging this relation into the first of the given equations, we have,
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.