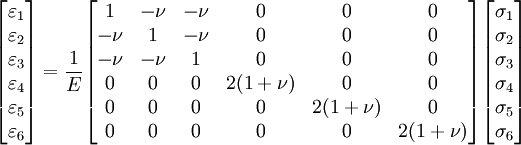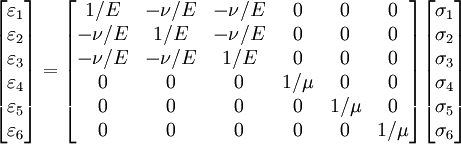Introduction to Elasticity/Constitutive example 5
< Introduction to ElasticityExample 5
Given:
An isotropic material with Young's modulus 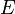 and Poisson's ration
and Poisson's ration 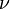 .
.
Find:
The compliance matrix of the material in terms of the Young's modulus and Poisson's ratio.
Solution
The strain is related to the stress via the compliance matrix by the equation
For an isotropic material
Therefore,
In engineering notation,
Converting into matrix notation,
We may also write the above equation as
where 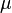 is the shear modulus.
is the shear modulus.
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

![\varepsilon_{ij} = \frac{1}{E}
\left[(1+\nu)\sigma_{ij} - \nu\sigma_{kk}\delta_{ij}\right]](../I/m/8778b1fb70b2ee1cba2c09315b0f0012.png)
![\begin{align}
\varepsilon_{11} & = \frac{1}{E}
\left[\sigma_{11} - \nu\sigma_{22} - \nu\sigma_{33}\right] \\
\varepsilon_{22} & = \frac{1}{E}
\left[\sigma_{22} - \nu\sigma_{11} - \nu\sigma_{33}\right] \\
\varepsilon_{33} & = \frac{1}{E}
\left[\sigma_{33} - \nu\sigma_{11} - \nu\sigma_{22}\right] \\
\varepsilon_{23} & = \frac{1}{E} \left[(1+\nu)\sigma_{23}\right] \\
\varepsilon_{31} & = \frac{1}{E} \left[(1+\nu)\sigma_{31}\right] \\
\varepsilon_{12} & = \frac{1}{E} \left[(1+\nu)\sigma_{12}\right]
\end{align}](../I/m/f4ed3e24574c25ccd17d1e654a129d29.png)
![\begin{align}
\varepsilon_{1} & = \frac{1}{E}
\left[\sigma_{1} - \nu\sigma_{2} - \nu\sigma_{3}\right] \\
\varepsilon_{2} & = \frac{1}{E}
\left[\sigma_{2} - \nu\sigma_{1} - \nu\sigma_{3}\right] \\
\varepsilon_{3} & = \frac{1}{E}
\left[\sigma_{3} - \nu\sigma_{1} - \nu\sigma_{2}\right] \\
\varepsilon_{4} & = \frac{1}{E} \left[2(1+\nu)\sigma_{4}\right] \\
\varepsilon_{5} & = \frac{1}{E} \left[2(1+\nu)\sigma_{5}\right] \\
\varepsilon_{6} & = \frac{1}{E} \left[2(1+\nu)\sigma_{6}\right]
\end{align}](../I/m/4c208e30ebe69a2ad845b29c944833a8.png)