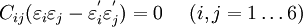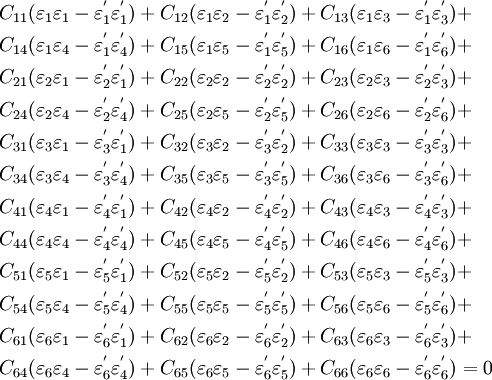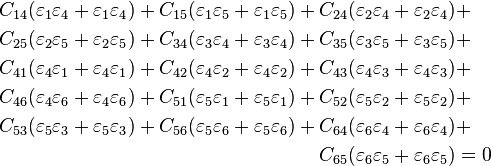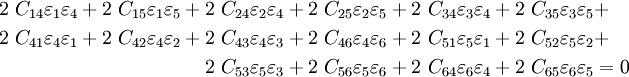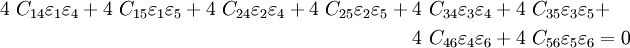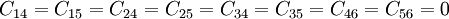Introduction to Elasticity/Constitutive example 4
< Introduction to ElasticityExample 4
Given:
A monoclinic crystal has inversion symmetric about the 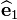 -
-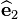 plane. Therefore, the material properties do not change for a mirror-reflection through this plane. The stress-strain relations must therefore remain unchanged under this transformation. The transformation matrix
plane. Therefore, the material properties do not change for a mirror-reflection through this plane. The stress-strain relations must therefore remain unchanged under this transformation. The transformation matrix ![\left[L\right]\,](../I/m/0f7eeb980099538ad8b49416d6b2a667.png) for this
for the mirror inversion is given by
for this
for the mirror inversion is given by
Show:
If we apply this transformation to the stress and strain tensors, then the stiffness matrix of the material (in Voigt notation) is
Solution
In 3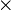 3 matrix form, the strain tensor is given by
3 matrix form, the strain tensor is given by
The transformation rule for a second order tensor 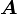 is
is
Applying this transformation to the strain tensor, we have
In engineering notation (Voigt notation),
Therefore, the transformed strain tensor can be written as
The expression for the strain energy density of a linear elastic material imposes a constraint on the components of the stiffness tensor in the presence of planes of material symmetry. This constraint is
where 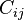 are the components of the 6
are the components of the 6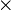 6 matrix that contains the independent components of the stiffness tensor.
6 matrix that contains the independent components of the stiffness tensor.
Therefore,
For a monoclinic material, replacing the transformed strain components by the equivalent original strain components, we get
or,
Using the symmetry of the stiffness matrix, we have
Since the strains can be arbitrary, the above condition is satisfied only if
Therefore, the stiffness matrix is given by
Hence shown.
![\left[L\right] = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1
\end{bmatrix}](../I/m/a71962569d17a3358d0e64caca9ab312.png)
![\left[C\right] = \begin{bmatrix}
C_{11} & C_{12} & C_{13} & 0 & 0 & C_{16} \\
C_{21} & C_{22} & C_{23} & 0 & 0 & C_{26} \\
C_{31} & C_{32} & C_{33} & 0 & 0 & C_{36} \\
0 & 0 & 0 & C_{44} & C_{45} & 0 \\
0 & 0 & 0 & C_{54} & C_{55} & 0 \\
C_{61} & C_{62} & C_{63} & 0 & 0 & C_{66} \\
\end{bmatrix}](../I/m/472a4f670b47ef852fd809bba33c3d68.png)
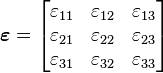
![\left[A\right]^{'} = \left[L\right] \left[A\right] \left[L\right]^{T}](../I/m/b9c456ff7c0809dcd85381daf522ba8d.png)
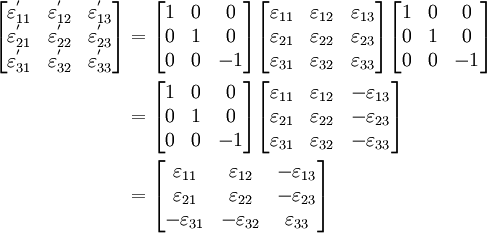
![\begin{align}
\left[\boldsymbol{\varepsilon}\right] & = \begin{bmatrix}
\varepsilon_{11} & \varepsilon_{22} & \varepsilon_{33} &
2\varepsilon_{23} & 2\varepsilon_{31} & 2\varepsilon_{12}
\end{bmatrix}^{T} \\
& = \begin{bmatrix}
\varepsilon_{1} & \varepsilon_{2} & \varepsilon_{3} &
\varepsilon_{4} & \varepsilon_{5} & \varepsilon_{6}
\end{bmatrix}^{T}
\end{align}](../I/m/d1b8e5acc165ba121d83c011ca02955b.png)
![\begin{align}
\left[\boldsymbol{\varepsilon}\right]^{'} & = \begin{bmatrix}
\varepsilon_{1}^{'} & \varepsilon_{2}^{'} & \varepsilon_{3}^{'} &
\varepsilon_{4}^{'} & \varepsilon_{5}^{'} & \varepsilon_{6}^{'}
\end{bmatrix}^{T} \\
& = \begin{bmatrix}
\varepsilon_{1} & \varepsilon_{2} & \varepsilon_{3} &
-\varepsilon_{4} & -\varepsilon_{5} & \varepsilon_{6}
\end{bmatrix}^{T} \\
\end{align}](../I/m/3b1eb3ba8277151a59a8cd465a627e32.png)