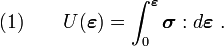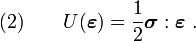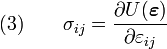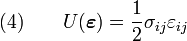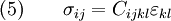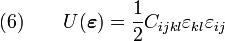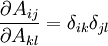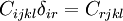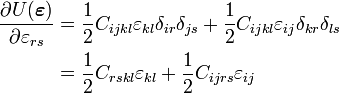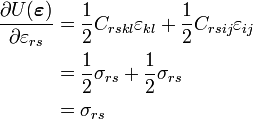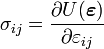Introduction to Elasticity/Constitutive example 3

Example 3

Given: The strain energy density for a material undergoing small strain

\text{(1)} \qquad U(\boldsymbol{\varepsilon}) = \int_0^{\boldsymbol{\varepsilon}} \boldsymbol{\sigma} : d\boldsymbol{\varepsilon}~.

Show: For linear elastic deformations and small strains,

\text{(2)} \qquad U(\boldsymbol{\varepsilon}) = \frac{1}{2} \boldsymbol{\sigma} : \boldsymbol{\varepsilon}~.

Solution

If the strain energy density is given by equation (1), then (for linear elastic materials) the stress and strain can be related using

\text{(3)} \qquad \sigma_{ij} = \frac{\partial U(\boldsymbol{\varepsilon})}{\partial \varepsilon_{ij}}

We will show that equation (2) is equivalent to equation (3). We start off with equation (2) and work backward.

\text{(4)} \qquad U(\boldsymbol{\varepsilon}) = \frac{1}{2} \sigma_{ij} \varepsilon_{ij}

For linear elastic materials,

\text{(5)} \qquad \sigma_{ij} = C_{ijkl} \varepsilon_{kl}

Substituting equation (5) into equation (4), we get,

\text{(6)} \qquad U(\boldsymbol{\varepsilon}) = \frac{1}{2} C_{ijkl} \varepsilon_{kl} \varepsilon_{ij}

Recall that, for a second order tensor $\boldsymbol{A}\,$ ,

\frac{\partial A_{ij}}{\partial A_{kl}} = \delta_{ik} \delta_{jl}

and that for a fourth order rensor 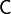$\mathsf{C}\,$ (substitution rule),

C_{ijkl} \delta_{ir} = C_{rjkl} \,

Differentiating equation (6) with respect to 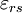$\varepsilon_{rs}\,$ , we have,

\begin{align} \frac{\partial U(\boldsymbol{\varepsilon})}{\partial \varepsilon_{rs}} & = \frac{1}{2} C_{ijkl} \varepsilon_{kl} \delta_{ir} \delta_{js} + \frac{1}{2} C_{ijkl} \varepsilon_{ij} \delta_{kr} \delta_{ls} \\ & = \frac{1}{2} C_{rskl} \varepsilon_{kl} + \frac{1}{2} C_{ijrs} \varepsilon_{ij} \end{align}

Using the symmetry of the stiffness tensor, we have,

\begin{align} \frac{\partial U(\boldsymbol{\varepsilon})}{\partial \varepsilon_{rs}} & = \frac{1}{2} C_{rskl} \varepsilon_{kl} + \frac{1}{2} C_{rsij} \varepsilon_{ij} \\ & = \frac{1}{2} \sigma_{rs} + \frac{1}{2} \sigma_{rs} \\ & = \sigma_{rs} \end{align}

Therefore,

\sigma_{ij} = \frac{\partial U(\boldsymbol{\varepsilon})}{\partial \varepsilon_{ij}}

which is the same as equation (3). Hence shown.

This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.