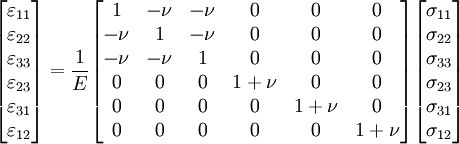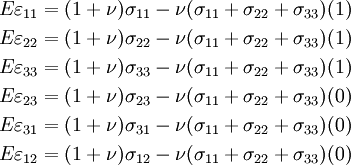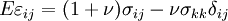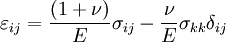Introduction to Elasticity/Constitutive example 2
< Introduction to ElasticityExample 1
Convert the stress-strain relation for isotropic materials (in matrix form) into an equation in index notation. Show all the steps in the process.
Solution
The stress-strain relation is
Let us expand out the terms and put all of them in a similar form. Thus,
We know that 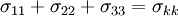 . Also a quantity that
is
. Also a quantity that
is 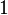 when
when 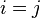 and
and 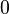 when
when 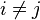 can be represented by the
Kronecker
can be represented by the
Kronecker 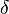 . Therefore, we can write the above equations as
. Therefore, we can write the above equations as
or,
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.