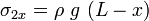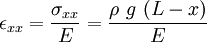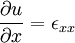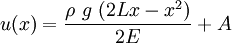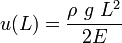Introduction to Elasticity/Constitutive example 1
< Introduction to ElasticityExample 1
Take a uniform bar of length "56", cross-section area "6", density "4", Young's modulus "8", and hang it from a rigid, hypothetical ceiling. Calculate how much the bar increases in length due to its own weight. Assume that the acceleration due to gravity is "6" and the bar is fixed rigidly to the ceiling.
Solution
The tensile stress at a point P, at a distance  from the ceiling is
from the ceiling is
From Hooke's law
Now,
Integrating,
Applying the boundary conditions, 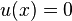 at
at 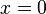 , we get
, we get 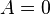 .
Therefore, the increase in length is
.
Therefore, the increase in length is
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.