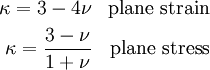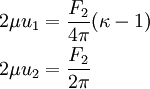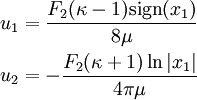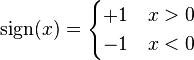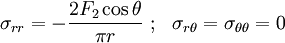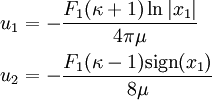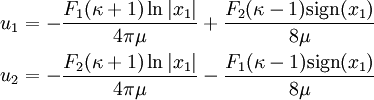Introduction to Elasticity/Concentrated force on half plane
< Introduction to ElasticityConcentrated Force on a Half-Plane
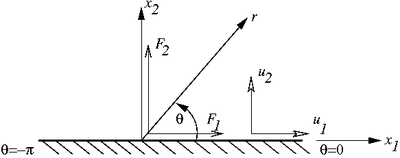 Concentrated force on a half plane |
From the Flamant Solution
and
If 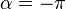 and
and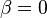 , we obtain the special case of
a concentrated force acting on a half-plane. Then,
, we obtain the special case of
a concentrated force acting on a half-plane. Then,
or,
Therefore,
The stresses are
The stress 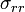 is obviously the superposition of the stresses
due to
is obviously the superposition of the stresses
due to 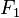 and
and 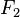 , applied separately to the half-plane.
, applied separately to the half-plane.
Problem 1: Stresses and displacements due to 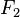
The tensile force 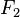 produces the stress field
produces the stress field
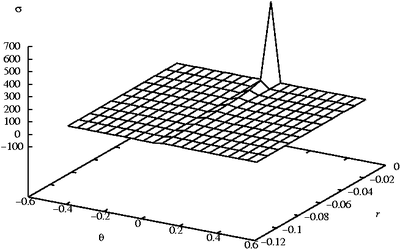 Stress due to concentrated force 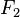 on a half plane on a half plane |
The stress function is
Hence, the displacements from Michell's solution are
At 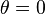 , (
, (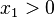 ,
, 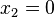 ),
),
At 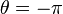 , (
, (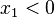 ,
, 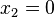 ),
),
where
Since we expect the solution to be symmetric about 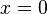 , we superpose a
rigid body displacement
, we superpose a
rigid body displacement
The displacements are
where
and 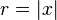 on
on 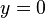 .
.
Problem 2: Stresses and displacements due to 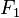
The tensile force 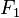 produces the stress field
produces the stress field
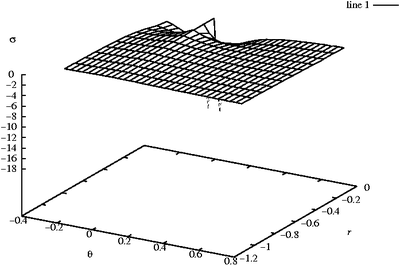 Stress due to concentrated force 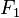 on a half plane on a half plane |
The displacements are
Stresses and displacements due to 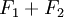
Superpose the two solutions. The stresses are
The displacements are
This article is issued from Wikiversity - version of the Wednesday, August 08, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
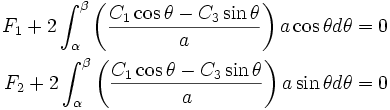
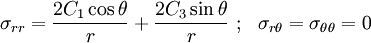
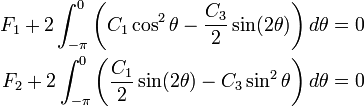
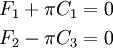
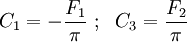
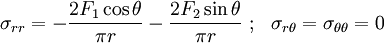
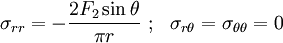
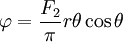
![\begin{align}
2\mu u_r & = \frac{F_2}{2\pi}\left[(\kappa-1)\theta\cos\theta +
\sin\theta - (\kappa+1)\ln(r)\sin\theta\right] \\
2\mu u_{\theta} & = \frac{F_2}{2\pi}\left[-(\kappa-1)\theta\sin\theta -
\cos\theta - (\kappa+1)\ln(r)\cos\theta\right]
\end{align}](../I/m/32d4b95d9da3e8266cb3865826c5e865.png)
![\begin{align}
2\mu u_r = 2\mu u_1 & = 0 \\
2\mu u_{\theta} = 2\mu u_2 & = \frac{F_2}{2\pi}\left[-1
- (\kappa+1)\ln(r)\right]
\end{align}](../I/m/42bde4cd8fe79bed502313810fa566f9.png)
![\begin{align}
2\mu u_r = -2\mu u_1 & =\frac{F_2}{2\pi}(\kappa-1)\\
2\mu u_{\theta} = -2\mu u_2 & = \frac{F_2}{2\pi}\left[1
+ (\kappa+1)\ln(r)\right]
\end{align}](../I/m/b6379cbff45736bba7b35034a69bced0.png)