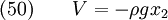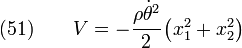Introduction to Elasticity/Body force potential
< Introduction to ElasticityBody force potential
How do we find the body force potential? Before we proceed let us examine what conservative vector fields are.
Conservative vector fields
- Work done in moving a particle from point A to point B in the field should be path independent.
- The local potential at point P in the field is defined as the work done to move a particle from infinity to P.
- For a vector field to be conservative
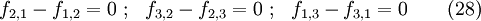
or
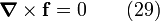
The field has to be irrotational.
Determining the body force potential
Suppose a body is rotating with an angular velocity 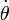 and an angular acceleration of
and an angular acceleration of 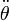 . Then,
. Then,
Let us assume that the 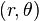 coordinate system is oriented at an angle
coordinate system is oriented at an angle 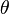 to the
to the 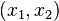 system. Then,
system. Then,
or,
or,
or,
If the origin is accelerating with an acceleration 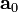 (for example, due to gravity), we have,
(for example, due to gravity), we have,
 :
:
The body force field is given by
For this vector body force field to be conservative, we require that,
Hence, the field 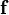 is conservative only if the rotational acceleration is zero, i.e. = the rotational velocity is constant.=
is conservative only if the rotational acceleration is zero, i.e. = the rotational velocity is constant.=
Now,
Hence,
Integrating equation (43),
Hence,
Integrating,
Without loss of generality, we can set 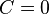 . Then,
. Then,
or,
For a body loaded by gravity only, we can set 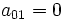 ,
, 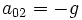 and
and 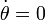 , to get
, to get
For a body loaded by rotational inertia only, we can set 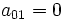 , and
, and 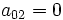 , and get
, and get
We can see that an Airy stress function + a body force potential of the form shown in equation (49) can be used to solve two-dimensional elasticity problems of plane stress/plane strain.
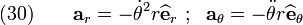
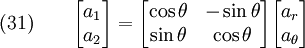
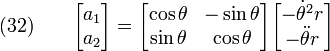
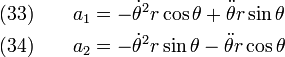
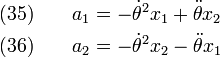
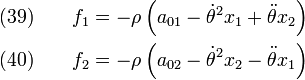
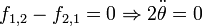
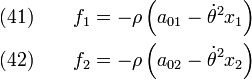
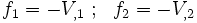
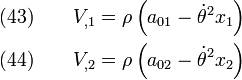
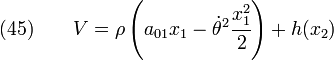
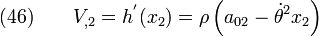
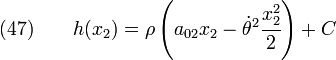
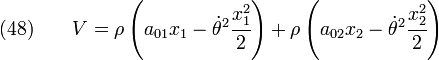
![\text{(49)} \qquad
V = \rho\left[a_{01} x_1 + a_{02} x_2 - \cfrac{\dot{\theta}^2}{2}
\left(x_1^2 + x_2^2\right)\right]](../I/m/ad137a1ef84268ff0b1fb924f00fa378.png)