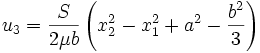Introduction to Elasticity/Beam bending example 1
< Introduction to ElasticityExample 1
Given:
A long rectangular beam with cross section 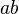
Find:
A solution for the displacement and stress fields, using strong boundary conditions on the edges 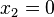 and
and
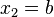 .
.
[Hint : Assume that the displacement can be expressed as a second degree polynomial (using the Pascal's triangle to determine the terms) 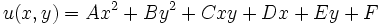 ]
]
Solution
Step 1: Boundary conditions
Step 2: Assume a solution
Let us assume antiplane strain
Step 3: Calculate the stresses
The stresses are given by 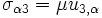 , and
, and 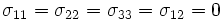 .
Therefore,
.
Therefore,
Step 4: Satisfy stress BCs
Thus we have,
Since 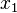 and
and 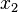 can be arbitrary,
can be arbitrary, 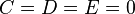 .
.
Hence, 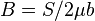 which gives us
which gives us
Assume that the body force is zero. Then the equilibrium condition is 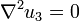 . Therefore,
. Therefore,
Therefore, the stresses are given by
Step 5: Satisfy displacement BCs
The displacement is given by
If we substitute 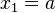 , we cannot determine the constant
, we cannot determine the constant 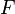 uniquely.
uniquely.
Hence the displacement boundary conditions have to be applied in a weak sense,
Therefore,
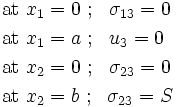
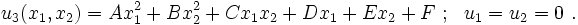
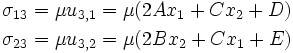
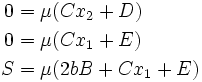
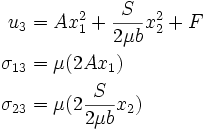
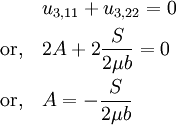
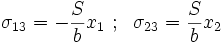
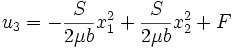
![\begin{align}
& \int_0^b u_3(a, x_2) dx_2 = 0 \\
\text{or,} \quad & \int_0^b \left(-\frac{S}{2\mu b}a^2 + \frac{S}{2\mu b}x_2^2 +
F\right) dx_2 = 0 \\
\text{or,} \quad & \left. \left[
\frac{S}{2\mu b} \left(-a^2 x_2 + \frac{x_2^3}{3}\right)
+ F x_2 \right]\right|_0^b = 0\\
\text{or,} \quad & \frac{S}{2\mu b} \left(-a^2 b + \frac{b^3}{3}\right)
+ F b = 0\\
\text{or,} \quad & \frac{S}{2\mu} \left(-a^2 + \frac{b^2}{3}\right) + Fb = 0\\
\text{or,} \quad & \frac{S}{2\mu} \left(-\frac{a^2}{b}+\frac{b}{3}\right)+ F = 0\\
\text{or,} \quad & F = \frac{S}{2\mu b} \left(a^2 - \frac{b^2}{3}\right)
\end{align}](../I/m/deabb8f21072da677c7c86bddb2ecdcd.png)