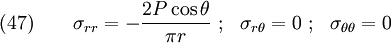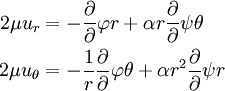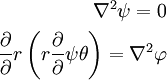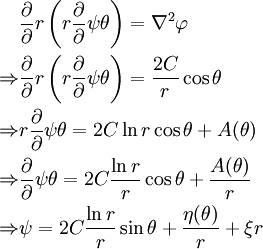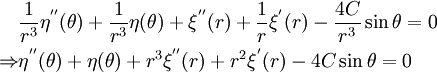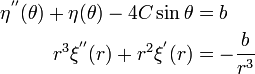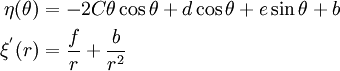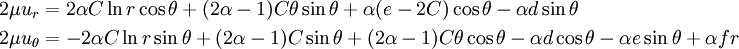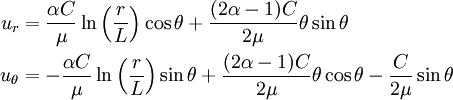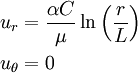Introduction to Elasticity/Axially loaded wedge
< Introduction to ElasticityAxially Loaded Wedge
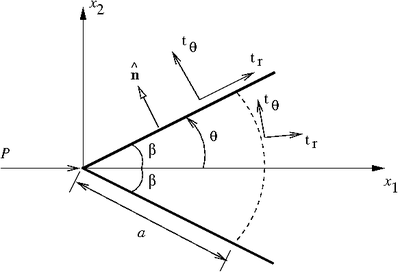 Elastic wedge loaded by an axial force |
The BCs at 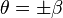 are
are
What about the concentrated force BC?
- What is
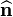 at the vertex ?
at the vertex ? - The traction is infinite since the force is applied on zero area. Consider equilibrium of a portion of the wedge.
At  , the BCs are
, the BCs are
For equilibrium, 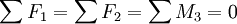 .
Therefore,
.
Therefore,
These constraint conditions are equivalent to the concentrated force BC.
Solution Procedure
Assume that 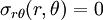 . This satisfies the traction
BCs on
. This satisfies the traction
BCs on 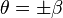 and equation (34). Therefore,
and equation (34). Therefore,
Hence,
That means 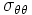 is independent of
is independent of 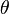 . Therefore,
in order to satisfy the BCs,
. Therefore,
in order to satisfy the BCs, 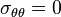 , i.e.,
, i.e.,
Checking for compatibility, 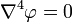 , we get
, we get
The general solution is
Therefore,
The only non-zero stress is 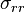 .
.
Plugging into equation (33), we get
Hence,
Plugging into equation (32), we get
Therefore,
The stress state is
Special Case : 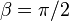
A concentrated point load acting on a half plane.
Displacements
where
Plug in 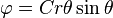 ,
,
Plug 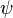 into
into 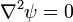 ,
,
Hence,
Solving,
Therefore,
To fix the rigid body motion, we set 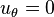 when
when 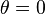 ,
and set
,
and set 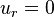 when
when 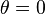 and
and 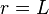 .Then,
.Then,
The displacements are singular at 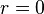 and
and 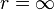 .
At
.
At 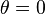 ,
,
Is the small strain assumption satisfied ?
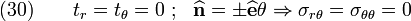
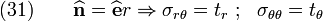
![\begin{align}
P_1 + \int_{-\beta}^{\beta} \left[ \sigma_{rr}(a,\theta)\cos\theta
- \sigma_{r\theta}(a,\theta)\sin\theta\right] a~d\theta = 0
\text{(32)} \qquad \\
\int_{-\beta}^{\beta} \left[ \sigma_{rr}(a,\theta)\sin\theta
+ \sigma_{r\theta}(a,\theta)\cos\theta\right] a~d\theta = 0
\text{(33)} \qquad \\
\int_{-\beta}^{\beta} \left[ a \sigma_{r\theta}(a,\theta)
\right] a~d\theta = 0
\text{(34)} \qquad
\end{align}](../I/m/622e06f6c69f98ae804a4a0b9a3565cb.png)
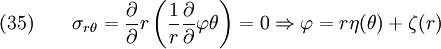
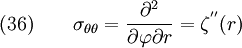
![\text{(37)} \qquad
\zeta(r) = C_1 r + C_2 \Rightarrow
\varphi = r\eta(\theta) + C_1 r = r[\eta(\theta)+C_1] = r\xi(\theta)](../I/m/d03a868021aeb599fb88c11b68148300.png)
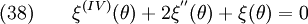
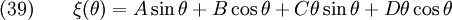
![\text{(40)} \qquad
{
\varphi = r\left[A\sin\theta + B\cos\theta + C\theta\sin\theta +
D\theta\cos\theta\right] }](../I/m/ec1c924c3d9f8b83d848ab3a00d03dbf.png)
![\text{(41)} \qquad
\sigma_{rr} = \frac{1}{r}\left[2C\cos\theta - 2D\sin\theta\right]](../I/m/11f7631b6975b8f96f6a10627b21b779.png)
![\text{(42)} \qquad
-D\left[2\beta - \sin(2\beta)\right] = 0 \Rightarrow D = 0](../I/m/00248cee0db58668ac5d2b29d676fc26.png)
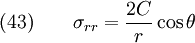
![\text{(44)} \qquad
-P = C\left[2\beta + \sin(2\beta)\right] \Rightarrow
C = \frac{-P}{2\beta+\sin(2\beta)}](../I/m/6b3197b5153028e34ca456031414da7d.png)
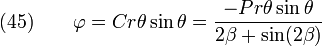
![\text{(46)} \qquad
{
\sigma_{rr} = -\frac{2P\cos\theta}{r[2\beta+\sin(2\beta)]} ~;~~
\sigma_{r\theta} = 0 ~;~~ \sigma_{\theta\theta} = 0
}](../I/m/b61d40a33e5e43adba2711fbb261bb8a.png)