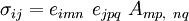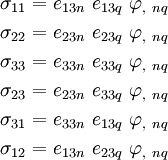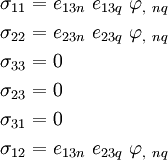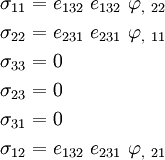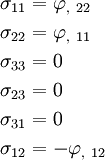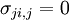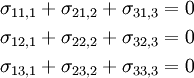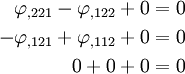Introduction to Elasticity/Airy example 1
< Introduction to ElasticityExample 1 - Beltrami solution
Given:
Beltrami's solution for the equations of equilibrium states that if
where  is a stress function, then
is a stress function, then
Airy's stress function is a special form of  , given by (in 3
, given by (in 3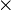 3 matrix notation)
3 matrix notation)
Show:
Verify that the stresses when expressed in terms of Airy's stress function satisfy equilibrium.
Solution
In index notation, Beltrami's solution can be written as
For the Airy's stress function, the only non-zero terms of 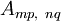 are
are 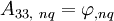 which can have nine values. Therefore,
which can have nine values. Therefore,
Since 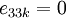 for
for 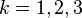 , the above set of equations reduces to
, the above set of equations reduces to
Now, 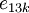 is non-zero only if
is non-zero only if  , and
, and 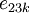 is non-zero
only if
is non-zero
only if  . Therefore, the above equations further reduce to
. Therefore, the above equations further reduce to
Therefore, (using the values of 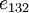 ,
, 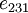 and the fact that the order of differentiation does not change the final result), we get
and the fact that the order of differentiation does not change the final result), we get
The equations of equilibrium (in the absence of body forces) are given by
or,
Plugging the stresses in terms of 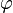 into the above equations gives,
into the above equations gives,
Noting that the order of differentiation is irrelevant, we see that equilibrium is satisfied by the Airy stress function.
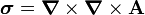
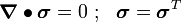
![\left[A\right] = \begin{bmatrix}
0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & \varphi
\end{bmatrix}](../I/m/73974ade6113b1365bc886f947112ec2.png)