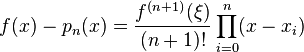Interpolation and Extrapolation
This course belongs to the track Numerical Algorithms in the Department of Scientific Computing in the School of Computer Science.
In this course, students will learn how to approximate discrete data. Different representations and techniques for the approximation are discussed.
Discrete Data
Discrete data arises from measurements of  or when
or when  is difficult or expensive to evaluate.
is difficult or expensive to evaluate.
In general, discrete data is given by a set of nodes 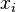 ,
, 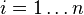 and the function
and the function  evaluated at these points:
evaluated at these points: 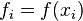 ,
, 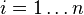 .
.
In the following, we will refer to the individual nodes and function values as 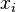 and
and 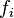 respectively. The vectors of the
respectively. The vectors of the  nodes or function values are written as
nodes or function values are written as 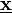 and
and 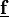 respectively.
respectively.
We will also always assume that the 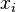 are distinct.
are distinct.
Polynomial Interpolation
Although there are many ways of representing a function  , polynomials are the tool of choice for interpolation.
As the Taylor series expansion of a function
, polynomials are the tool of choice for interpolation.
As the Taylor series expansion of a function  around
around 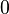 shows, every continuous, differentiable function has a polynomial representation
shows, every continuous, differentiable function has a polynomial representation
in which the 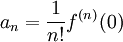 are the exact weights.
are the exact weights.
If a function  is assumed to be continuous and differentiable and we assume that it's derivatives
is assumed to be continuous and differentiable and we assume that it's derivatives 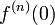 are zero or of negligible magnitude for increasing
are zero or of negligible magnitude for increasing  , it is a good idea to approximate the function with a polynomial.
, it is a good idea to approximate the function with a polynomial.
Given  distinct nodes
distinct nodes 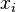 ,
, 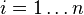 at which the function values
at which the function values 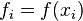 are known, we can construct an interpolating polynomial
are known, we can construct an interpolating polynomial 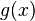 such that
such that 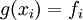 for all
for all 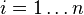 . Such an interpolating polynomial with degree
. Such an interpolating polynomial with degree 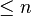 is unique. However infinitely many such polynomials can be found with degree
is unique. However infinitely many such polynomials can be found with degree 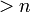 .
.
- Any nice way of deriving the interpolation error?
The Vandermonde Matrix
By definition as given above, our polynomial
must interpolate the function  at the
at the  nodes
nodes 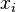 . This leads to the following system of
. This leads to the following system of  linear equations in the coefficients
linear equations in the coefficients 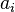 :
:
We can re-write this system of linear equation in matrix notation as
where 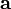 is the vector of the
is the vector of the 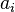 ,
,  coefficients and
coefficients and 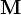 is the so-called moment matrix or Vandermonde matrix with
is the so-called moment matrix or Vandermonde matrix with
or
This linear system of equations can be solved for 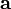 using Gauss elimination or other methods.
using Gauss elimination or other methods.
The following shows how this can be done in Matlab or GNU Octave.
% declare our function f
f = inline('sin(pi*2*x)','x')
% order of the interpolation?
n = 5
% declare the nodes x_i as random in [0,1]
x = rand(n,1)
% create the moment matrix
M = zeros(n)
for i=1:n
M(:,i) = x.^(i-1);
end
% solve for the coefficients a
a = M \ f(x)
% compute g(x)
g = ones(n,1) * a(1)
for i=2:n
g = g + x.^(i-1)*a(i);
end;
% how good was the approximation?
g - f(x)
However practical it may seem, the Vandermonde matrix is not especially suited for more than just a few nodes. Due to it's special structure, the Condition Number of the Vandermode matrix increases with  .
.
If in the above example we set 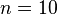 and compute
and compute 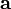 with
with
% solve for the coefficients a a = inv(M) * f(x)
the approximation is only good up to 10 digits. For 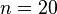 it is accurate only to one digit.
it is accurate only to one digit.
We must therefore consider other means of computing and/or representing 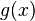 .
.
Lagrange Interpolation
Given a set of  nodes
nodes 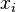 ,
, 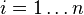 , we define the
, we define the 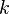 th Lagrange Polynomial as the polynomial of degree
th Lagrange Polynomial as the polynomial of degree 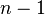 that satisifies
that satisifies
Maybe add a nice plot of a Lagrange polynomial over a few nodes?
The first condition, namely that 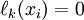 for
for 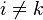 can be satisfied by construction. Since every polynomial of degree
can be satisfied by construction. Since every polynomial of degree 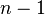 can be represented as the product
can be represented as the product
where the 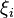 are the roots of
are the roots of 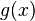 and
and  is some constant, we can construct
is some constant, we can construct 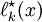 as
as
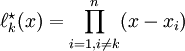 .
.
The polynomial 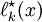 is of order
is of order 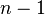 and satisifies the first condition, namely that
and satisifies the first condition, namely that 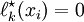 for
for 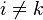 .
.
Since, by construction, the 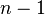 roots of
roots of 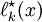 are at the nodes
are at the nodes 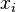 ,
, 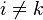 , we know that the value of
, we know that the value of 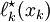 cannot be zero. This value, however, should be
cannot be zero. This value, however, should be 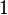 by definition. We can enforce this by scaling
by definition. We can enforce this by scaling 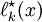 by
by 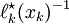 :
:
If we insert any 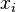 ,
, 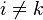 into the above equation, the nominator becomes
into the above equation, the nominator becomes 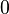 and the first condition is satisified. If we insert
and the first condition is satisified. If we insert 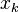 , the nominator and the denominator are the same and we get
, the nominator and the denominator are the same and we get 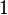 , which means that the second condition is also satisfied.
, which means that the second condition is also satisfied.
We can now use the Lagrange polynomials 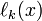 to construct a polynomial
to construct a polynomial 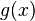 of degree
of degree 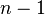 which interpolates the
which interpolates the  function values
function values 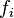 at the points
at the points 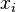 .
.
Consider that, given the definition of 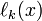 ,
,
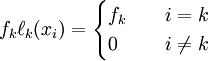 .
.
Therefore, if we define 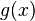 as
as
then 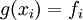 for all
for all 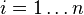 . Since the
. Since the 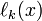 are all of degree
are all of degree 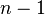 , the weighted sum of these polynomials is also of degree
, the weighted sum of these polynomials is also of degree 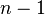 .
.
Therefore, 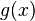 is the polynomial of degree
is the polynomial of degree 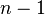 which interpolates the
which interpolates the  values
values 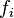 at the nodes
at the nodes 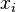 .
.
The representation with Lagrange polynomials has some advantages over the monomial representation 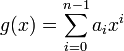 described in the previous section.
described in the previous section.
First of all, once the Lagrange polynomials have been computed over a set of nodes 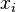 , computing the interpolating polynomial for a new set of function values
, computing the interpolating polynomial for a new set of function values 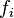 is trivial, since these only need to be multiplied with the Lagrange polynomials, which are independent of the
is trivial, since these only need to be multiplied with the Lagrange polynomials, which are independent of the 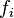 .
.
Another advantage is that the representation can easily be extended if additional points are added. The Lagrange polynomial 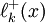 , obtained by adding a point
, obtained by adding a point 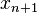 to the interpolation, is
to the interpolation, is
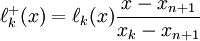 .
.
Only the new polynomial 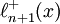 would need to be re-computed from scratch.
would need to be re-computed from scratch.
In the monomial representation, adding a point would involve adding an extra line and column to the Vandermonde matrix and re-computing the solution.
- Add a word on Barycentric interpolation to facilitate adding points.
Newton Interpolation
Given a set of  function values
function values 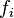 evaluated at the nodes
evaluated at the nodes 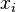 , the Newton polynomial is defined as the sum
, the Newton polynomial is defined as the sum
where the 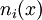 are the
are the  Newton basis polynomials defined by
Newton basis polynomials defined by
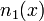

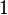
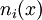

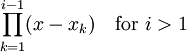 .
.
An interpolation polynomial of degree n+1 can be easily obtained from that of degree n by just adding one more node point 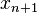 and adding a polynomial of degree n+1 to
and adding a polynomial of degree n+1 to 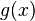 .
.
The Newton form of the interpolating polynomial is particularly suited to computations by hand, and underlies Neville's algorithm for polynomial interpolation. It is also directly related to the exact formula for the error term 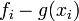 . Any good text in numerical analysis will prove this formula and fully specify Neville's algorithm, usually doing both via divided differences.
. Any good text in numerical analysis will prove this formula and fully specify Neville's algorithm, usually doing both via divided differences.
(Should link to error formula, divided differences and Neville's algorithm, adding articles where they don't exist)
Interpolation error
When interpolating a given function f by a polynomial of degree n at the nodes x0,...,xn we get the error
where
is the notation for divided differences.
If f is n + 1 times continuously differentiable on a closed interval I and 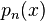 be a polynomial of degree at most n that interpolates f at n + 1 distinct points {xi} (i=0,1,...,n) in that interval. Then for each x in the interval there exists
be a polynomial of degree at most n that interpolates f at n + 1 distinct points {xi} (i=0,1,...,n) in that interval. Then for each x in the interval there exists 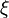 in that interval such that
in that interval such that
The above error bound suggests choosing the interpolation points xi such that the product | Π (x − xi) | is as small as possible.
Proof
Let's set the error term is
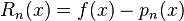
and set up a auxiliary function 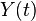 and the function is
and the function is
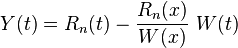
where
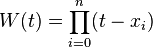
and
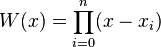
Since 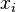 are roots of function f and
are roots of function f and 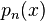 , so we will have
, so we will have
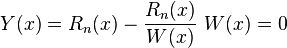
and
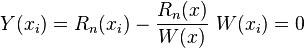
Then 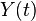 has n+2 roots. From Rolle's theorem,
has n+2 roots. From Rolle's theorem, 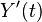 has n+1 roots, then
has n+1 roots, then 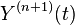 has one root
has one root 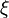 , where
, where 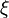 is in the interval I.
is in the interval I.
So we can get
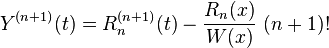
Since  is a polynomial of degree at most n, then
is a polynomial of degree at most n, then
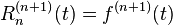
Thus
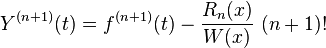
Since 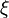 is the root of
is the root of 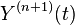 , so
, so
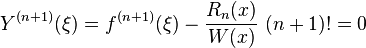
Therefore
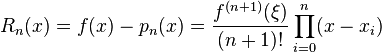 .
.
Piecewise Interpolation / Splines
Extrapolation
Interpolation is the technique of estimating the value of a function for any intermediate value of the independent variable while the process of computing the value of the function outside the given range is called extrapolation.
Caution must be used when extrapolating, as assumptions outside the data region (linearization, general shape and slope) may breakdown.
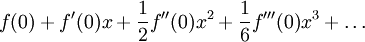
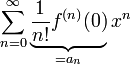
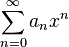
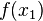
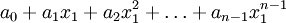
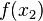
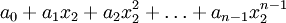
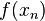
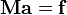
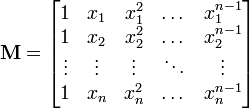

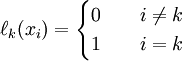
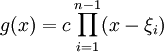
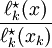
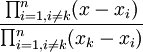
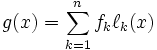
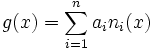
![f(x) - p_n(x) = f[x_0,\ldots,x_n,x] \prod_{i=0}^n (x-x_i)](../I/m/699f8146765a3d9651c264c1bfc8c8da.png)
![f[x_0,\ldots,x_n,x]](../I/m/f1c9e47c69d12dc1826f544b55c0efdd.png)