Integrating factors

Educational level: this is a tertiary (university) resource.

Resource type: this resource is a lesson.

Subject classification: this is a mathematics resource .

Completion status: this resource is ~25% complete.

School:Mathematics > Topic:Differential_Equations > Ordinary Differential Equations > Integrating Factors

Definition

If the expression 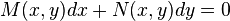$M(x,y) dx + N(x,y) dy = 0$ is not exact or homogeneous, an integrating factor 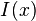$I(x)$ can be found so that the equation:

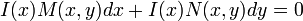
$I(x)M(x,y) dx + I(x)N(x,y) dy = 0$

is exact.

Solution

There are 2 approaches to a solution.

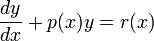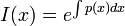If the function is of the form $\frac {dy}{dx}+p(x)y=r(x)$ , then the integrating factor is $I(x)=e^{\int p(x) dx}$ .

OR

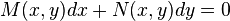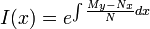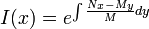If the function is of the standard form $M(x,y)dx+N(x,y)dy=0$ , then the integrating factor is $I(x)=e^{\int \frac {M_y-N_x}{N} dx}$ or $I(x)=e^{\int \frac {N_x-M_y}{M} dy}$ .
Substitute the integration factor into the equation 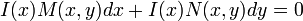$I(x)M(x,y)dx+I(x)N(x,y)dy=0$ and solve.

This article is issued from Wikiversity - version of the Saturday, July 09, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.