Numbers/Integers
< Numbers
The integers (from the Latin integer, literally "untouched", hence "whole": the word entire comes from the same origin, but via French[1]) are formed by the natural numbers including 0 (0, 1, 2, 3, ...) together with the negatives of the non-zero natural numbers (−1, −2, −3, ...). Viewed as a subset of the real numbers, they are numbers that can be written without a fractional or decimal component, and fall within the set {..., −2, −1, 0, 1, 2, ...}. For example, 21, 4, and −2048 are integers; 9.75 and 5½ are not integers. The set of all integers is often denoted by a blackboard bold 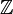 , which stands for Zahlen (German for numbers). [2] The integers (with addition as operation) form the smallest group containing the additive monoid of the natural numbers. Like the natural numbers, the integers form a countably infinite set. Integers can be thought of as discrete, equally spaced points on an infinitely long number line. In algebraic number theory, these commonly understood integers, embedded in the field of rational numbers, are referred to as rational integers to distinguish them from the more broadly defined algebraic integers (but with "rational" meaning "quotient of integers", this attempt at precision suffers from circularity).
, which stands for Zahlen (German for numbers). [2] The integers (with addition as operation) form the smallest group containing the additive monoid of the natural numbers. Like the natural numbers, the integers form a countably infinite set. Integers can be thought of as discrete, equally spaced points on an infinitely long number line. In algebraic number theory, these commonly understood integers, embedded in the field of rational numbers, are referred to as rational integers to distinguish them from the more broadly defined algebraic integers (but with "rational" meaning "quotient of integers", this attempt at precision suffers from circularity).
Elementary properties of the integers
- Negative numbers
- Number line with negative numbers
- Addition of positive and negative whole numbers
- Subtraction of positive and negative whole numbers
- Multiplication and division of positive and negative whole numbers
Algebraic properties
Like the natural numbers, Z is closed under the operations of addition and multiplication, that is, the sum and product of any two integers is an integer. However, with the inclusion of the negative natural numbers, and, importantly, zero, Z (unlike the natural numbers) is also closed under subtraction. Z is not closed under division, since the quotient of two integers (e.g., 1 divided by 2), need not be an integer. Although the natural numbers are closed under exponentiation, the integers are not (since the result can be a fraction when the exponent is negative).
The following lists some of the basic properties of addition and multiplication for any integers a, b and c.
|
|
Addition |
Multiplication |
|
Closure: |
a + b is an integer |
a × b is an integer |
|
Associativity: |
a + (b + c) = (a + b) + c |
a × (b × c) = (a × b) × c |
|
Commutativity: |
a + b = b + a |
a × b = b × a |
|
Existence of an identity element: |
a + 0 = a |
a × 1 = a |
|
Existence of inverse elements: |
a + (−a) = 0 |
1 × 1 = 1 = (−1) × (−1) Only ±1 have inverses in Z. |
|
Distributivity: |
a × (b + c) = (a × b) + (a × c) |
(a + b) × c = (a × c) + (b × c) |
|
No zero divisors: |
If a × b = 0, if and only if a = 0 or b = 0 (or both). |
|
In the language of abstract algebra, the first five properties listed above for addition say that Z under addition is an abelian group. In addition, the first four properties listed above say that Z is an abelian monoid with respect to both addition and multiplication. As a group under addition, Z is a cyclic group, since every nonzero integer can be written as a finite sum 1 + 1 + ... + 1 or (−1) + (−1) + ... + (−1). In fact, Z under addition is the only infinite cyclic group, in the sense that any infinite cyclic group is isomorphic to Z.
The first four properties listed above for multiplication say that Z under multiplication is a commutative monoid. However not every integer has a multiplicative inverse; e.g. there is no integer x such that 2x = 1, because the left hand side is even, while the right hand side is odd. This means that Z under multiplication is not a group.
All the rules from the above property table, except for the last, taken together say that Z together with addition and multiplication is a commutative ring with unity. Adding the last property says that Z is an integral domain. In fact, Z provides the motivation for defining such a structure.
The lack of multiplicative inverses, which is equivalent to the fact that Z is not closed under division, means that Z is not a field. The smallest field containing the integers is the field of rational numbers. This process can be mimicked to form the field of fractions of any integral domain.
Although ordinary division is not defined on Z, it does possess an important property called the division algorithm: that is, given two integers a and b with b ≠ 0, there exist unique integers q and r such that a = q × b + r and 0 ≤ r < | b |, where | b | denotes the absolute value of b. The integer q is called the quotient and r is called the remainder, resulting from division of a by b. This is the basis for the Euclidean algorithm for computing greatest common divisors.
Again, in the language of abstract algebra, the above says that Z is a Euclidean domain. This implies that Z is a principal ideal domain and any positive integer can be written as the products of primes in an essentially unique way. This is the fundamental theorem of arithmetic.
Construction
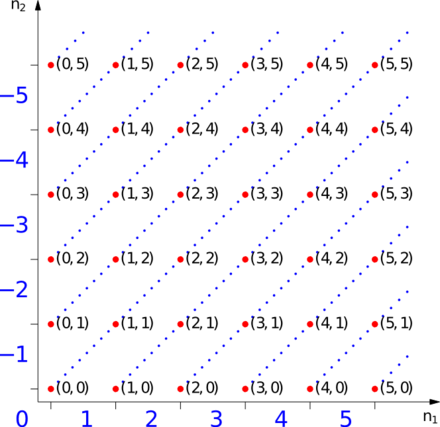
The integers can be formally constructed as the equivalence classes of ordered pairs of natural numbers (a, b).[3]
The intuition is that (a, b) stands for the result of subtracting b from a. To confirm our expectation that 1 − 2 and 4 − 5 denote the same number, we define an equivalence relation ~ on these pairs with the following rule:
precisely when
Addition and multiplication of integers can be defined in terms of the equivalent operations on the natural numbers; denoting by [(a,b)] the equivalence class having (a,b) as a member, one has:
The negation (or additive inverse) of an integer is obtained by reversing the order of the pair:
Hence subtraction can be defined as the addition of the additive inverse:
The standard ordering on the integers is given by:
![[(a,b)]<[(c,d)]\,](../I/m/cd20ff73f10fdb26cb05a241b4888d03.png) iff
iff 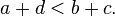
It is easily verified that these definitions are independent of the choice of representatives of the equivalence classes.
Every equivalence class has a unique member that is of the form (n,0) or (0,n) (or both at once). The natural number n is identified with the class [(n,0)] (in other words the natural numbers are embedded into the integers by map sending n to [(n,0)]), and the class [(0,n)] is denoted −n (this covers all remaining classes, and gives the class [(0,0)] a second time since −0 = 0.
Thus, [(a,b)] is denoted by
If the natural numbers are identified with the corresponding integers (using the embedding mentioned above), this convention creates no ambiguity.
This notation recovers the familiar representation of the integers as {... −3,−2,−1, 0, 1, 2, 3, ...}.
Some examples are:
References
- ↑ Evans, Nick (1995). "A-Quantifiers and Scope". In Bach, Emmon W. Quantification in Natural Languages. Dordrecht, The Netherlands; Boston, MA: Kluwer Academic Publishers. pp. 262. ISBN 0792333527. http://books.google.com/?id=NlQL97qBSZkCTemplate:Inconsistent citations
- ↑ Miller, Jeff (2010-08-29). "Earliest Uses of Symbols of Number Theory". Retrieved 2010-09-20.
- ↑
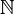 2, the set of ordered pairs of natural numbers, is defined as the Cartesian product
2, the set of ordered pairs of natural numbers, is defined as the Cartesian product 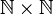 where
where 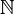 = {0,1,2,3,…} is the set of natural numbers.
= {0,1,2,3,…} is the set of natural numbers.
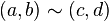
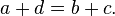
![[(a,b)]+[(c,d)] := [(a+c,b+d)].\,](../I/m/bf337cc180aaafed2c987a227b799e47.png)
![[(a,b)]\cdot[(c,d)] := [(ac+bd,ad+bc)].\,](../I/m/28866cf8c27afb7c817dc2d64fcbbd58.png)
![-[(a,b)] := [(b,a)].\,](../I/m/0cca34240f5c542ab8397f1b9a9a55ff.png)
![[(a,b)]-[(c,d)] := [(a+d,b+c)].\,](../I/m/92d53b5e8a5cac307bcf01f3f798b402.png)
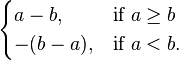
![\begin{align}
0 &= [(0,0)] &= [(1,1)] &= \cdots & &= [(k,k)] \\
1 &= [(1,0)] &= [(2,1)] &= \cdots & &= [(k+1,k)] \\
-1 &= [(0,1)] &= [(1,2)] &= \cdots & &= [(k,k+1)] \\
2 &= [(2,0)] &= [(3,1)] &= \cdots & &= [(k+2,k)] \\
-2 &= [(0,2)] &= [(1,3)] &= \cdots & &= [(k,k+2)].
\end{align}](../I/m/1c72a33a064c334c308c4c8ea4539b15.png)