Ideas in Geometry/Area

3.2.1 Areas

There are simple equations to find the area of common shapes such as the triangle or parallelogram.

Heron's Formula

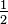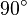We learn at a young age that the area of a triangle can be expressed by the equation $\tfrac{1}{2}$ base $\cdot$ height. This uses two sides of a triangle on either side of an angle but sometimes it can be difficult to find the height of a triangle that is perpendicular to the base, creating a $90^\circ$ angle, which is what you need for the usual formula for the area of a triangle. But there is also a way to find the area of a triangle using the lengths of all three sides. This can be expressed in Heron's Formula where the area can be found using the equation 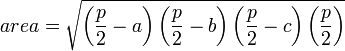$area= \sqrt {\left (\frac{p}{2} -a \right) \left (\frac{p}{2}-b \right) \left (\frac{p}{2} -c \right) \left (\frac{p}{2} \right)}$ where a,b &c represent the sides of the triangle and p=a+b+c, the perimeter of the triangle.

Here is an example to show what we mean:

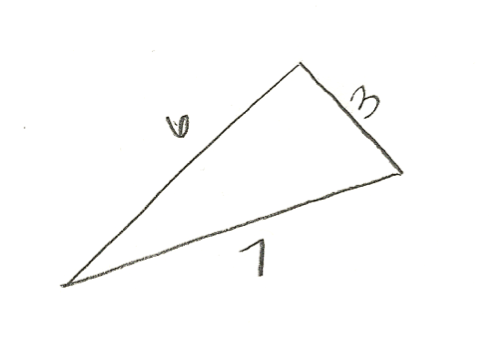
To find the area of this triangle, we would use the equation with the sides lengths: 3,6 & 7 and find the area --> p=16 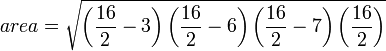$area= \sqrt {\left (\frac{16}{2} -3 \right) \left (\frac{16}{2}-6 \right) \left (\frac{16}{2} -7 \right) \left (\frac{16}{2} \right)}$ and we would get the answer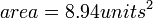 $area=8.94 units^2$

A Quadrilateral Circumscribed in a Circle

If we know that there is a formula that works for triangles given the three lengths of the sides, we can find a formula in a similar way for the area of a quadrilateral. As long as the quadrilateral can be circumscribed in a circle, which means each vertex touches the inside of the circle and the opposite angles must sum to 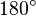$180^\circ$ , the area of the quadrilateral can be solved. See picture below of a quadrilateral circumscribed in a circle.

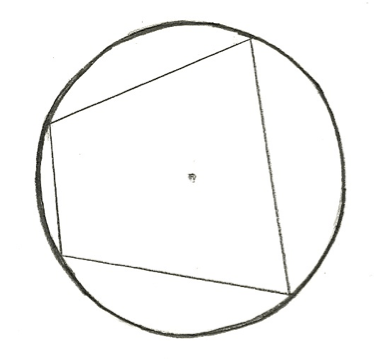
Brahmagupta's Formula

In this formula, Brahmagupta's Formula, if given a quadrilateral that can be circumscribed in a circle (also known as cyclic), the area of the quadrilateral can be expressed by the equation: 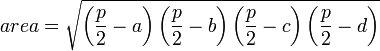$area= \sqrt {\left (\frac{p}{2} -a \right) \left (\frac{p}{2}-b \right) \left (\frac{p}{2} -c \right) \left (\frac{p}{2}-d \right)}$ , where a,b,c & d represent the sides of the quadrilateral and p=a+b+c+d, the perimeter of the quadrilateral.

Here is an example to show what we mean:

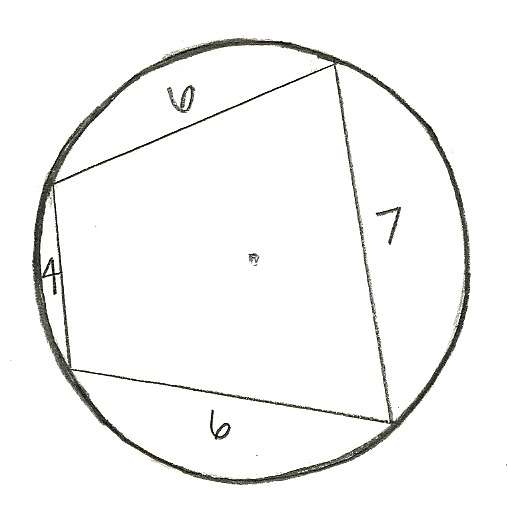
Using these side lengths: 4, 6, 6, & 7, we would use the formula to find the area --> p=23 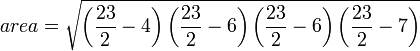$area= \sqrt {\left (\frac{23}{2} -4 \right) \left (\frac{23}{2}-6 \right) \left (\frac{23}{2} -6 \right) \left (\frac{23}{2}-7 \right)}$ and get the answer to be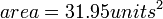 $area=31.95 units^2$

Lattice Points

There is also a way of finding the area of shapes besides triangles and quadrilaterals that involves lattice points. Lattice points are points that are spaced 1 unit apart, horizontally and vertically in a plane. Here are some lattice points:

Pick's Theorem

If the vertices of a polygon are located on the lattice points, we can find the area of the polygon by using Pick's Theorem: 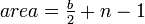$area=\tfrac{b}{2} + n - 1$ where b=the number of lattice points on the border of the polygon and n=the number of lattice points on the inside of the polygon. Here is an example:

Since the vertices of the polygon lie on the lattice points, we can use Pick's Theorem. So in this example: b=15, n=14. And 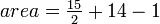$area=\tfrac{15}{2} + 14 - 1$ . So the area=20.5 square units.

This article is issued from Wikiversity - version of the Saturday, August 16, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.