Homogeneous differential equations

Educational level: this is a tertiary (university) resource.

Resource type: this resource is a lesson.

Subject classification: this is a mathematics resource .

Completion status: this resource is ~25% complete.

School:Mathematics > Topic:Differential_Equations > Ordinary Differential Equations > Homogeneous Differential Equations

Homogeneous

Definition

The word “homogeneous” can mean different things depending on what kind of differential equation you’re working with. A homogeneous equation in this sense is defined as one where the following relationship is true:

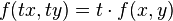
$\textstyle f(tx,ty) = t \cdot f(x,y)$

Solution

The solution to a homogeneous equation is to:

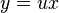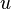Use the substitution $\textstyle y = ux$ where $u$ is a substitution variable.
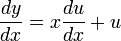Implicitly differentiate the above equation to get $\frac {dy} {dx} = x \frac {du} {dx} + u$ .
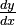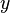Replace $\textstyle \frac {dy} {dx}$ and $\textstyle y$ with these expressions.
Solve for $u$ .
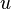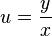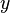Substitute with the expression $u = \frac {y} {x}$ Then solve for $\textstyle y$ .

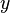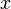The advantage of this method is that the function is in terms of 2 variables, but we simplify the equation by relating $\textstyle y$ and $\textstyle x$ to each other.

This article is issued from Wikiversity - version of the Saturday, July 09, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.