Function
A function, also known as map, transformation, operator and morphism, is an object that uniquely maps input (aka domain) values onto a corresponding point in the output (co-)domain. Saying formally, function f it is a subset of the Cartesian product X×Y, f ⊂ X×Y such that for every x in X there is only one pair (x,y) contained in f. This uniqueness of the mapping: there is only one output value y for a given input x.
One writes
- f(x) = y
or
- f: X → Y
or simply f(x) if relation (x,y) is in f. The elements of input domain, x-es, are called arguments of the function and the target elements, y = f(x), are called the values (or result) of the function. Supplying an argument to the function is called valuation, evaluation of mathematical expression at specific point or function application.
The notation f: f: X → Y is addresses the type of the argument and result whereas f(x) = y specifies the names of the argument and result. The name of the result 'y' is often identified with function name 'f' itself. In programming, we can usually specify both argument/value name and type, e.g
def f(x: X): Y = ???
says that function f takes one argument of type X and produces result of type Y in Scala and types specify/constrain the range of values that function can take or produce.
Defining and representing functions
You can plot the functions whose arguments and values are numeric. For instance
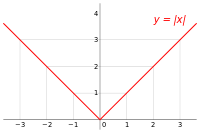
| x: | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y: | 3 | 2 | 1 | 0 | 1 | 2 | 3 |
maps argument -3 → value 3, -2→2, .., 2→2 and 3→3. If you mark x values on the horizontal axis and go vertically up the height that corresponds to the numerical value of the function, y, for that x, marking a dot for every (x,y) couple, your dots must be located on the red line plotted on the right.
The function defined by the table is discrete and finite. It maps a finite amount of points. There are also continuous functions, the ones whose domain is countable infinite. You cannot use table to define such a function. The analytic form is used in this case, eg. y = x², for a square function.
Multivalued input and output
A function may have more than one argument. For instance summation
- +: a,b → sum
has two arguments and can be denoted by +(a,b). However, you can treat (a,b) as a single composite object, i.e. a vector. Similarly, you can treat w:multivalued functions: since, strictly speaking, a "well-defined" function associates one and only one output to any particular input, you are in trouble defining e.g. a square root function since, for any number except 0 there are two results, e.g. both +2 and -2 squared give 4. In this case it is convenient to think that the function produces a set, {-2,+2}.
Vectors
Basically vectors and functions are the same thing. The only difference is that argument is called index in case of vector and vectors are more often discrete and by dimension of function you mean the amount of arguments it has where as vector dimension is the cardinality of the index range. For instance, vector [1,8,3] is a function that maps 0→1, 1→8 and 2→3.
This is further elaborated in the operator theory, where operators stand for higher order functions, which means that they are functions over functions. For instance, differentiation is an operator, it e.g. translates a function sin(x) → cos(x). The operators are often finitely discrete and represented in matrix form in this case by rectangles whereas vectors are single columns and by, dot product, operator (a function) translates a vector (a function) into another vector (another function).
Since you can multiply the function by a scaler, s (in this case the function values will be s times larger/smaller), and add functions together arriving at another function, the functions can be referred to as vectors in linear algebra.
Subprograms in programming
The algorithms are normally programmed into subprograms in programming. Look at the function as a black box that maps input to output whereas the procedure in the internals, the real mechanism that implements the mapping. The point is that you may have many different implementations/algorithms of the same function.
Another differentiation between the procedures and functions in programming is that function, in contrast to procedure, always returns a single value whereas procedures do not return anything -- they just modify the visible state variables/files. Such mutation of system state is known as side effects. Functions, on the other hand can be pure. They are called pure if never access the state, neither to read nor write it.
Pure functions are appreciated in functional programming, which also uses higher order functions (recall operators and functions over functions). Functional purity simplifies the analysis of program behaviour but also makes functions valid mathematical objects, since the fact that result of such functions is independent on the state of the system means that it depends only on the argument, which means that it invariably produces the same result, for the same arguments. Functional programming admits w:partial application, when one some but not all arguments supplied to the function.
Typically, programmers define functions like
def debug(title: String, x: Int) = title + " x = " + x.toString
which contain both funciton name, every argument name and type and procedure body. In programming and computer science you can also define anonymous functions, often called lambda expressions. For instance, λx.x+2 is a lambda-expression which defines a function x+2 of single variable x. Here λ means "we define a function" and x is its single argument name, without the type.