Fourier transforms
The Fourier Transform represents a function 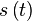 as a "linear combination" of complex sinusoids at different frequencies
as a "linear combination" of complex sinusoids at different frequencies 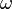 . Fourier proposed that a function may be written in terms of a sum of complex sine and cosine functions with weighted amplitudes.
. Fourier proposed that a function may be written in terms of a sum of complex sine and cosine functions with weighted amplitudes.
In Euler notation the complex exponential may be represented as:
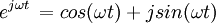
Thus, the definition of a Fourier transform is usually represented in complex exponential notation.
The Fourier transform of s(t) is defined by
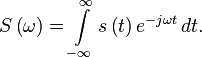
Under appropriate conditions original function can be recovered by:
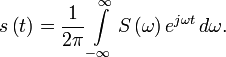
The function  is the Fourier transform of
is the Fourier transform of  . This is often denoted with the operator
. This is often denoted with the operator  , in the case above,
, in the case above, 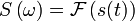
The function 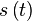 must satisfy the Dirichlet conditions in order for
must satisfy the Dirichlet conditions in order for 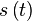 for the integral defining Fourier transform to converge.
for the integral defining Fourier transform to converge.
Forward Fourier Transform(FT)/Anaysis Equation
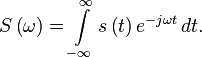
Inverse Fourier Transform(IFT)/Synthesis Equation
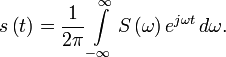
Relation to the Laplace Transform
In fact, the Fourier Transform can be viewed as a special case of the bilateral Laplace Transform. If the complex Laplace variable s were written as 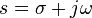 , then the Fourier transform is just the bilateral Laplace transform evaluated at
, then the Fourier transform is just the bilateral Laplace transform evaluated at 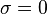 . This justification is not mathematically rigorous, but for most applications in engineering the correspondence holds.
. This justification is not mathematically rigorous, but for most applications in engineering the correspondence holds.
Properties
| × | Time Function | Fourier Transform | Property |
|---|---|---|---|
| 1 | 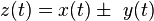 | 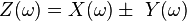 | Linearity |
| 2 | 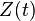 | 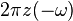 | Duality |
| 3 | 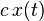 , c = constant , c = constant | 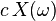 | Scalar Multiplication |
| 4 | 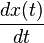 | 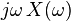 | Differentiation in time domain |
| 5 | 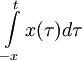 | 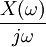 , if , if 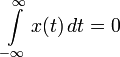 | Integration in Time domain |
| 6 | 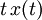 | 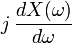 | Differentiation in Frequency Domain |
| 7 | 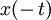 | 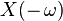 | Time reversal |
| 8 | 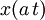 | 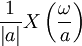 | Time Scaling |
| 9 | 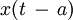 | 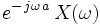 | Time shifting |
| 10 | 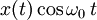 | ![\frac{1}{2}\left [ X(\omega\,+\,\omega_0)\,+\,X(\omega\,-\,\omega_0) \right ]](../I/m/e4dce17e15bc6b35f1ef593c8f7966f0.png) | Modulation |
| 11 | 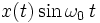 | ![\frac{1}{2j}\left [ X(\omega\,-\,\omega_0)\,-\,X(\omega\,+\,\omega_0) \right ]](../I/m/2a1d4ea2d0358b1d393f75a1d0866d76.png) | Modulation |
| 12 | 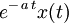 | 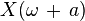 | Frequency shifting |
| 13 | 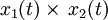 | 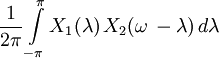 | Convolution |