Formal language theory/Parallel replacement systems

< Formal language theory

Parallel replacement systems

A foray into the language theoretic aspects of Lindenmayer systems. For D0L systems, we have followed the presentation in Salomaa's book[1].

A D0L (deterministic, zero context) system 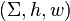(\Sigma, h, w) over an alphabet 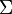\Sigma consists of a start string 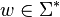w \in \Sigma^{*} and a single replacement rule given by a homomorphism 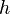h. These systems have perhaps surprising properties.

Question: What happens when 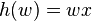h(w) = wx for some string x?


Hierachies

0L: instead of a homomorphism, there is a finite substitution

Question: Find a language that is in 0L but not in D0L. (this is not hard)

DTOL: instead of a single homomorphism, there is a table 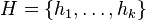H=\{h_1, \dots, h_k\} of homomorphisms

Question: Find a language that is in DT0L but not in D0L or 0L.


Further Reading

Books

[2]

  1. ↑ Arto Salomaa, Jewels in Formal Language Theory, Computer Science Press 1981
  2. ↑ Rozenberg and Salomaa, The Mathematical Theory of L Systems
  Formal language theory/Parallel replacement systems is a stub. Learn how you can help Wikiversity to expand it.
This article is issued from Wikiversity - version of the Friday, January 04, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.