Formal language theory/Homomorphisms

Homomorphisms

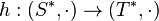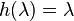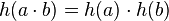Monoid homomorphisms, $h : (S^{*}, \cdot) \rightarrow (T^{*}, \cdot)$ , $h(\lambda) = \lambda$ and $h(a\cdot b)=h(a)\cdot h(b)$ , can be extended to languages 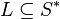$L \subseteq S^{*}$ in one way that is compatible with set union, 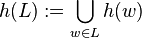$h(L) := \bigcup\limits_{w \in L} h(w)$ , to make a basic tool in formal language theory, allowing for renaming and simple replacements of letters.

Special homomorphisms include the non-deleting ones (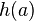 $h(a)$ is never 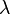$\lambda$ ) and the letter-to-letter ones (the image of each letter is a single letter).

A generalisation of this, the replacement of each letter by a whole language is not in general a homomorphism, it is a substitution.

This article is issued from Wikiversity - version of the Friday, January 04, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.