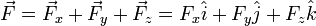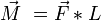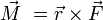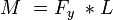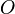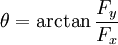Force systems
Part of the Statics course offered by the Division of Applied Mechanics, School of Engineering and the Engineering and Technology Portal
Lecture
Force is a component of dynamics, which describes the causes of motion. Dynamics is in turn part of Newtonian Mechanics in the large field of Physics. Force systems are also the starting point of engineering analysis.
Force Vectors
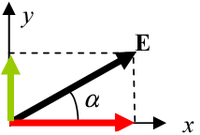
A force vector is a force defined in two or more dimensions with a component vector in each dimension which may all be summed to equal the force vector. Similarly, the magnitude of each component vector, which is a scalar quantity, may be multiplied by the unit vector in that dimension to equal the component vector.
Moment
For a system wherein a rigid body experiences a force F at a orthogonal distance L from a fixed point, the moment M is the quantity (oddly enough of the same units as energy) defined by the force multiplied by the length of distance between the fixed point and the point where the force is applied. The direction of the moment is perpendicular to the force ecotro and the length, using the right hand rule.
In the event that a force impacts the rigid body at an angle other than a right angle 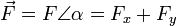 , the moment is determined by the component of the force vector
, the moment is determined by the component of the force vector 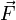 that is orthogonal to the length L.
that is orthogonal to the length L.
The general case in three dimensions can be calculated with the cross product. Do note that the order of the distance vector 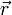 and the force
and the force  does matter in cross products as opposite order will change signs.
does matter in cross products as opposite order will change signs.
The components of a moment vector is the moment around the respective axis, following the right hand rule.
Example:
M = Force * Length = 100 Newtons * 10 Meters = 1,000 Newton-meters (N-m)
Example: Force F is incident on the end of a rigid body of length L at an angle A degrees from the central axis of the body x (Hint: draw a free body diagram).
Thenand
Couple
A couple is a pair of equal and opposite force vectors that are some distance apart and that act upon the same body, thus causing a rotation.
Imagine that force 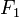 and force
and force 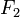 are incident at two locations along a rigid body of total length
are incident at two locations along a rigid body of total length 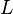 at positions
at positions 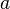 and
and 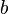 , where
, where 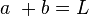 .
(Hint: draw a free body diagram)
.
(Hint: draw a free body diagram)
Then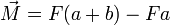
In 3D the same rule applies, using that
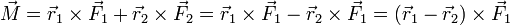 which means that the moment will be the same around any point in the system.
which means that the moment will be the same around any point in the system.
Resultant
Any system of forces may be reduced to a system of components and a resulting moment.
That is to say,and
about the point
and
and
and then
with
...thenis magnitude
in the direction of
Assignments
Activities:
- Create an activity
Readings:
- Peruse the appropriate sections of b:Statics
Study guide:
- Wikipedia article:Force System
- Wikipedia article:Vector
- Wikipedia article:Force Vector
- Wikipedia article:Moment
- Wikipedia article:Couple
- Wikipedia article:Resultant