Fluid Mechanics for Mechanical Engineers/Transport Equations
< Fluid Mechanics for Mechanical EngineersDiffusion Phenomena
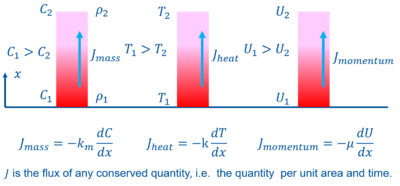
The fluid motion (convection) takes place with two mechanisms:
- The advective flow, which is the bulk motion of the fluid in a certain direction.
- The molecular motion, which persists to exist even if there is no convection.
The molecular motion is responsible for the diffusion phenomena. In fluid mechannics, we consider mostly the diffusion of mass, momentum and energy.
The diffusion of a quantity takes place always from rich to poor regions. For example, when one puts a drop of ink in water, ink molecules moves (diffuses) from ink rich region to ink poor region. Heat diffuses from high temperature regions to colder regions. Similarly, momentum diffuses from momentum rich regions to momentum poor regions. The diffusive flux in one diemension is formulated by Fick's first law as follows for mass, energy and momentum respectively:
![J_{m}=-k_m\frac{d C}{d x} [\frac{kg}{m^2s}] \quad \text{where} \quad C \quad \text{is the concentration with the unit} \quad [mol/m^3] .](../I/m/f42b11af60e782c7dbc2ad8cee6493b8.png)
![J_{E}=-k\frac{d T}{d x} [\frac{J}{m^2s}]](../I/m/3f649a7d00370273036f2d3c03e2c2f8.png)
![J_{mom}=-\mu\frac{d U}{d x} [\frac{kg\,m/s}{m^2s}]](../I/m/922b96d9cd3c2b3dfb3c7b318df29a87.png)
The negative sign is used since the gradient is negative opposite to the direction of diffusion, i.e. with the negative sign the direction of diffusion is correctly assesed. The constants of diffusion are the diffusion constant of one species into another, thermal conductivity and the dynamic viscosity of the fluid, respectively. The diffusion of energy in the form of heat is also called as conduction.
General Form of Transport Equations
The RTT theorem is given only with advection and without any sources. In the more general form of transport equation, the diffusion and the sources of the transported quantities have to be considered. For an extensive quantity 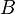 , the transport equation is:
, the transport equation is:
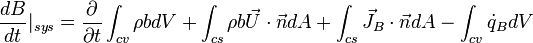
where 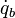 is the source of
is the source of 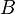 per unit volume within CV and
per unit volume within CV and 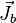 is the diffusive flux of
is the diffusive flux of 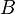 through the CS of CV.
through the CS of CV.
Conservation of Mass Equation (Continuity Equation)
The integral equation for the conservation of mass law is
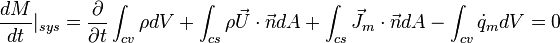
According to this equation, when adjective and diffusive flux are ignored, it can be seen that the rate of change of mass in the CV is due to the mass sources:
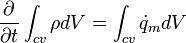 In case of no adjective flux and mass sources,
In case of no adjective flux and mass sources,
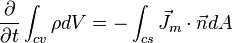 the mass in CV, can change only through diffusive flux. Note that, incoming diffusive flux will have a negative sign and together with the extra negative sign its contribution will be positive.
the mass in CV, can change only through diffusive flux. Note that, incoming diffusive flux will have a negative sign and together with the extra negative sign its contribution will be positive.
For a differential volume 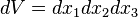 , each term in the integral equation can be formulated as follows:
, each term in the integral equation can be formulated as follows:
The time rate of change of mass in the CV: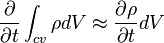
The advective flow rate of mass through CS:
The advective flow rate can be decomposed into the surfaces having their surface normal vectors along  ,
, 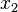 and
and 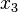 axis:
axis: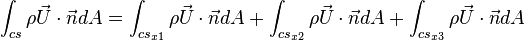
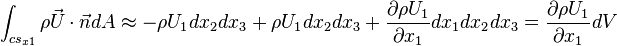 Hence the total advective flux is:
Hence the total advective flux is:
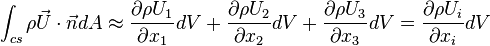 In fact, one can see clearly the Divergence theorem:
In fact, one can see clearly the Divergence theorem:
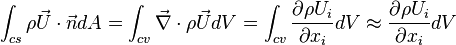 The diffusive flow rate of mass through CS:
The diffusive flow rate of mass through CS:
By using the divergence theorem, the diffusive flow rate can be written for a differential volume as follows:
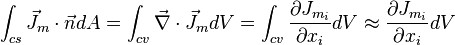 For isotropic diffusion, the
For isotropic diffusion, the 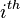 component of the diffusion flux is
component of the diffusion flux is
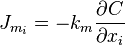 Hence the diffusive flow rate can be written as
Hence the diffusive flow rate can be written as
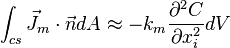
The net source of mass in CV:
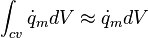 The final differential form of the conservation of mass equation reads
The final differential form of the conservation of mass equation reads
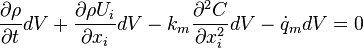 and per nunit volume
and per nunit volume
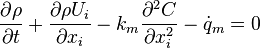
Conservation of Energy Equation
The conservation of energy equaiton is very interesting since it shows the dissipation of energy and reversible conversion of energy as the fluid flows. The transport equation of energy reads:
![{\displaystyle
\displaystyle \frac{dE}{dt}|_{sys} =[\dot{Q}+\dot{W}]_{on\ sys}= \frac{\partial}{\partial t}\int_{cv}{\rho e dV} + \int_{cs}{\rho e \vec{U}\cdot\vec{n}dA}+\int_{cs}{\vec{J}_E\cdot\vec{n}dA}-\int_{cv}{\dot{q}_E dV}
}](../I/m/a2ae8e1804abdc3bccb22fee4cc59f50.png) where
where 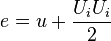 is the sum of internal energy and kinetic energy per unit mass.
is the sum of internal energy and kinetic energy per unit mass.
Rearranging the above equaiton for an instant at whşch CV and the system collapse on each other:
![{\displaystyle
\frac{\partial}{\partial t}\int_{cv}{\rho e dV} + \int_{cs}{\rho e \vec{U}\cdot\vec{n}dA}=[\dot{Q}+\dot{W}]_{on\ cv}-\int_{cs}{\vec{J}_E\cdot\vec{n}dA}+\int_{cv}{\dot{q}_E dV}
}](../I/m/49fd945954ee2e9c038ca2b111908021.png) Heat
Heat 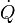 can be added to the CV in the form of radiation or a surface heater. The source of energy
can be added to the CV in the form of radiation or a surface heater. The source of energy 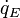 can be the energy released or absorbed during chemical reaction or the energy of the added mass from the source of mass. Therefore,
can be the energy released or absorbed during chemical reaction or the energy of the added mass from the source of mass. Therefore, 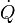 can be treated as a part of energy source
can be treated as a part of energy source 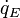 if it is a volumetric addition and/or as a part of conduction
if it is a volumetric addition and/or as a part of conduction 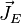 term on the surface of the CV if it is a heating surface.
term on the surface of the CV if it is a heating surface.
The rate of change of energy in a differential volume is
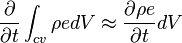
The advection term for a differential volume can be formulated by using the divergence theorem
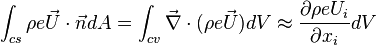 Body and surface forces work on CV
Body and surface forces work on CV 
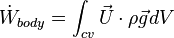
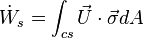 where
where 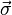 is the sum of the stress caused by pressure and viscous stresses
is the sum of the stress caused by pressure and viscous stresses
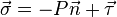 Hence,
Hence,
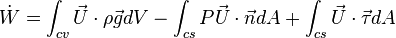 Since
Since 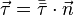 is the local stress vector and
is the local stress vector and 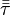 is the stress tensor.
is the stress tensor.
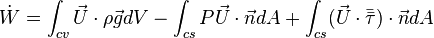
For a diffrential volume, 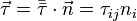 is the stress vector on a face having its nomal in
is the stress vector on a face having its nomal in 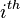 -direction.
-direction.
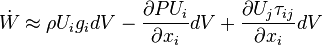 In order to have a better decomposition later, one can switch
In order to have a better decomposition later, one can switch 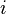 and
and 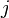 index since
index since  and use the equality
and use the equality 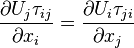
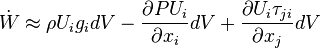
The heat diffusion (conduction) term for a differential volume can be written by using the divergence term as:
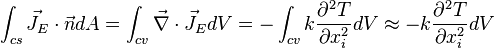 Rewriting the energy equation, using the above forms derived for a differential volume:
Rewriting the energy equation, using the above forms derived for a differential volume:
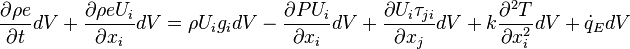 or per unit volume
or per unit volume
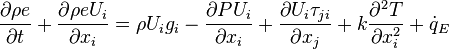
When left side of the equation is expanded,
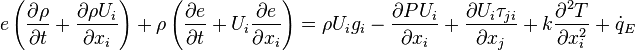 it can be seen that the first term involves one part of the conservation of mass equation. Neglecting the diffusion and source of mass, the continuity equation can be set to zero and the energy equation can be reduced to:
it can be seen that the first term involves one part of the conservation of mass equation. Neglecting the diffusion and source of mass, the continuity equation can be set to zero and the energy equation can be reduced to:
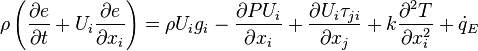 The left side becomes the substantial derivative of the energy per unit time:
The left side becomes the substantial derivative of the energy per unit time:
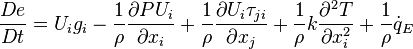
Decomposition of Energy Equation
Inserting the definition of 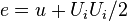 and expanding the work done by pressure and viscous stresses,
and expanding the work done by pressure and viscous stresses,
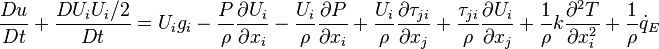 Since
Since 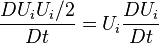 ,
,
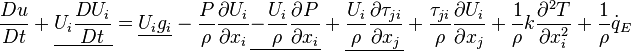 Now we can decompose this equation into the mechanical and thermal energy equations. The underlined terms are nothing but the scalar product of the velocity vector and the momentum equation
Now we can decompose this equation into the mechanical and thermal energy equations. The underlined terms are nothing but the scalar product of the velocity vector and the momentum equation 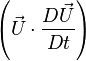 and form the mechanical energy equation, the remaining terms form the thermal energy equation.
and form the mechanical energy equation, the remaining terms form the thermal energy equation.
The mechanical energy equation: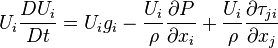 Since
Since 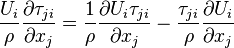 and
and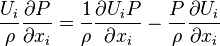 The mechanical energy equation can be written in a more interpretable manner:
The mechanical energy equation can be written in a more interpretable manner:
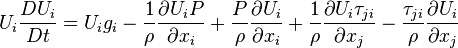 The thermal energy equation:
The thermal energy equation: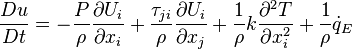 The meaning of each term is as follows:
The meaning of each term is as follows:
| Term | Physical meaning |
|---|---|
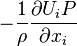 |
Rate of work done by pressure. |
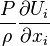 |
Rate of reversible conversion of kinetic energy into internal energy. (-) in the case of compression and (+) in the case of expansion, because 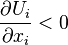 for compression and larger than 0 for expansion. It appears with a negative sign in the internal energy equation. for compression and larger than 0 for expansion. It appears with a negative sign in the internal energy equation. |
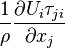 |
Rate of work done by viscous stresses. |
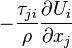 |
Rate of dissipation of mechanical energy, in other words irreversible conversion of kinetic energy to internal energy. It is always negative. In other words, mechanical energy drops due to this term. In the internaş energy equation it appears with a possitive sign. |
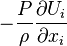 |
Rate of reversible conversion of kinetic energy into internal energy. (+) in the case of compresion and (-) in the case of expansion, because 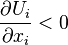 for compression and larger than 0 for expansion. for compression and larger than 0 for expansion. |
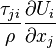 |
Rate of increase of internal energy by irreversible viscous dissipation. It is always positive. In other words, internal energy increases due to this term. |
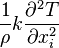 |
Rate of heat added or extracted via conduction (thermal diffusion). It can be (+) or (-). |
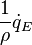 |
Rate of head added via combustion or radiation. |
Comment on the dissipation term
The dissipation term
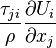 is always positive and extracts energy from the mechanical energy equation and inreases the internal energy. As can be seen, without the viscous stresses or velocity gradients there is no dissipation. In fact, viscous stresses do occur only when there is a velocişty gradient. Hence, in order to avoid dissipation one should avoid or reduce unnecessary velocity gradients.
is always positive and extracts energy from the mechanical energy equation and inreases the internal energy. As can be seen, without the viscous stresses or velocity gradients there is no dissipation. In fact, viscous stresses do occur only when there is a velocişty gradient. Hence, in order to avoid dissipation one should avoid or reduce unnecessary velocity gradients.