Fluid Mechanics for MAP/Fluid Statics
< Fluid Mechanics for MAPDefinitions
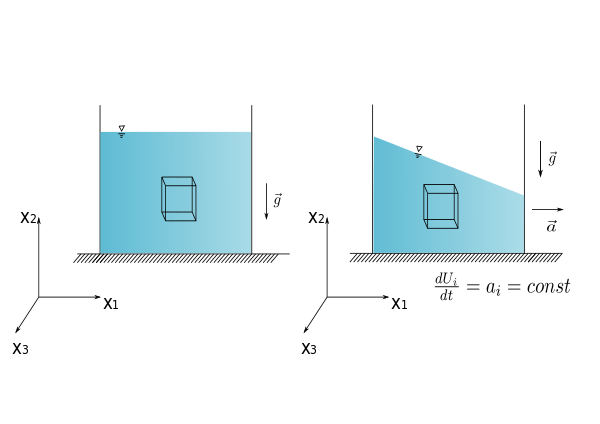
Fluid statics is the study of fluids which are either at rest or in rigid body motion with respect to a fixed frame of reference. Rigid body motion means that there is no relative velocity between the fluid particles.
In a fluid at rest, there is no shear stress, i. e. fluid does not deform, but fluid sustains normal stresses.
We can apply Newton's second law of motion to evaluate the reaction of the particle to the applied forces.
Force balance in 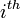 direction:
direction:
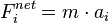
We can also say,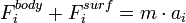
Force created by pressure is :
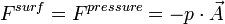
 is the vector having the surface area as magnitude and surface normal as direction.
is the vector having the surface area as magnitude and surface normal as direction.
Thus,
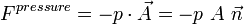
Force caused by the pressures opposite to the surface normal.
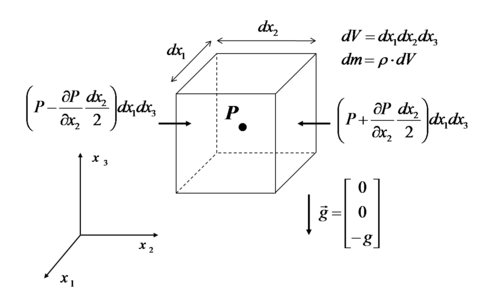
For a differential fluid element:
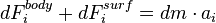
Remember Taylor Series expansion:
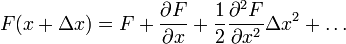
P is the pressure in the center of the fluid element, therefore the pressure on the surface in direction of 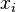 is
is 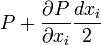 .
.
Thus,
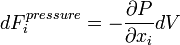
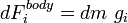
Thus,
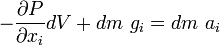 or,
or,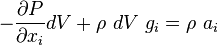
or,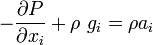
or,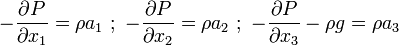
for 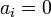
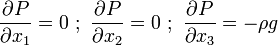
Pressure changes only in 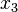 direction.
direction.
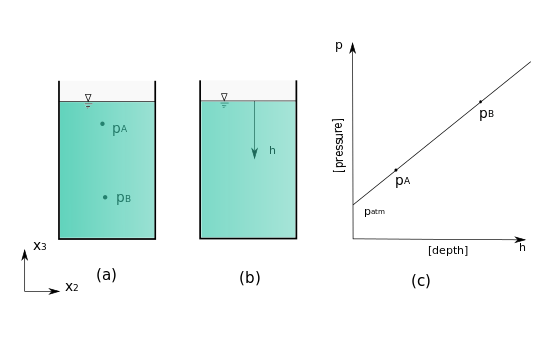
Pressure variation in an incompressible and static fluid
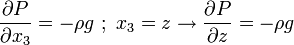 is constant since
is constant since 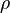 and
and 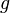 are constants.
are constants.
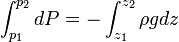
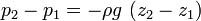
If we take 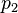 at the surface, then:
at the surface, then:
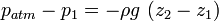
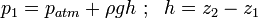
h is measured from the surface.
|
Any two points at the same elevation in a continuous length of the same liquid are at the same pressure. Pressure increases as one goes down in a liquid column. Remember: 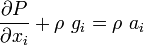 |
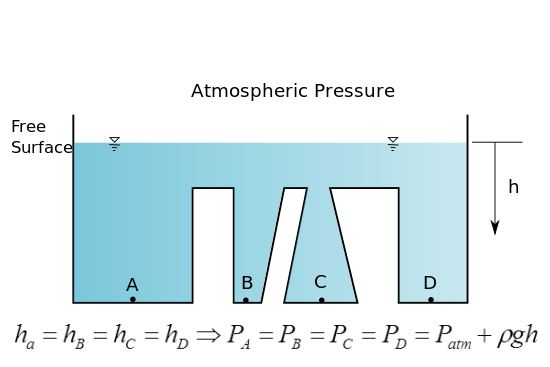 similar depth in same fluid experience similar hydrostatic pressure |
|
For incompressible flow, 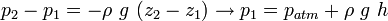 Consider 3 immiscible fluids in a container and find out a relation for the pressure at the bottom of the fluid shown in the schematics besides.
|
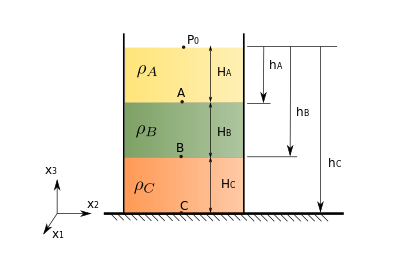 Hydrostatic pressure profile for fluids with different densities and height |
Transmission of Pressure
|
Concept of transmission of pressure is very important for hydraulic and pneumatics system. Neglecting elevation changes the following relation can be written: 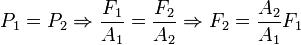 which could be stated in the famous Pascal's law like below: A change in pressure at any point in an enclosed fluid at rest is transmitted undiminished to all points in the fluid |
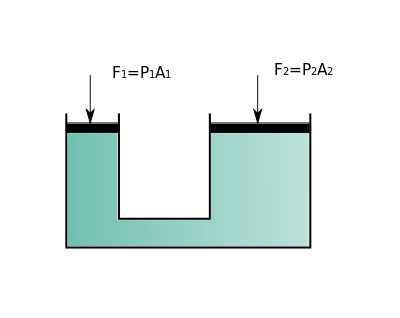 Pascal's law |
Communicating containers
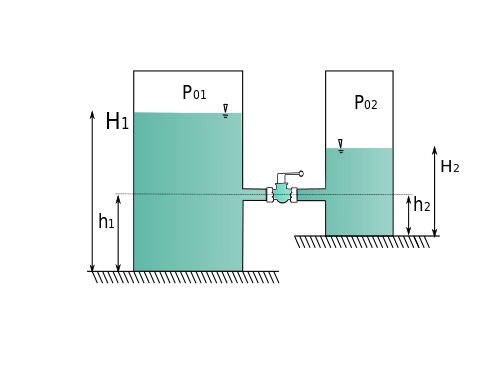
|
Lets consider two closed containers(which means the free surface pressure could be different than atmospheric pressure) both contain same fluid are connected via a connector valve. When the valve is open, the heights of the fluid columns can give an indication about the pressure in both chamber. For closed container 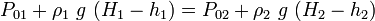 (of course,when we calculate the small 'h', it should be measured at the height of connecting valve for both column distinctively.) for 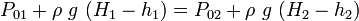 So from the picture above, we can understand that the pressure in the right column is higher than the left column. For open Containers,
If both fluid columns are at the same level
so, the depth of the fluid from free surface in both column will be the same. This nice principle was used for Water-based Barometer [1] a.k.a 'Storm Barometer' or 'Goethe Barometer'. Try to see if you understand the device. |
 Goethe Barometer |
Pressure Measurement Equipments
Barometer
|
From the equations which we derived before , it is also possible to measure the pressure exerted by almost 100 km[2] thick earth atmosphere which is above us. Since the constituents and the density varies over the height of the atmosphere , we will consider a fluid column which have free surface with no atmospheric pressure but connected with a fluid which experience atmospheric pressure like communicating container. Let consider first (from previous section), 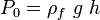 for water height will be: 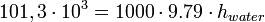
|
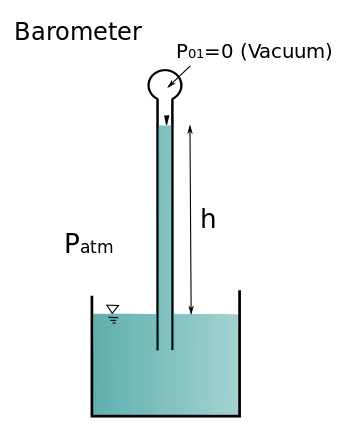 Barometer |
U-tube manometer
|
The volume rate of flow, Q, through a pipe can be determined by means of a flow nozzle located in the pipe as illustrated in the figure. The nozzle creates a pressure drop, (a) Although the fluid in the pipe is moving, the fluids in the columns of the manometer are at rest so that the pressure variation in the manometer tubes is hydrostatic. If we start at point A and move vertically upward to level (1), the pressure will decrease by Thus, in equation form 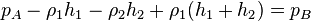 or 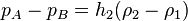 It is to be noted that the only column height of importance is the differential reading,
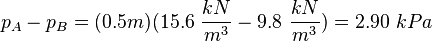 |
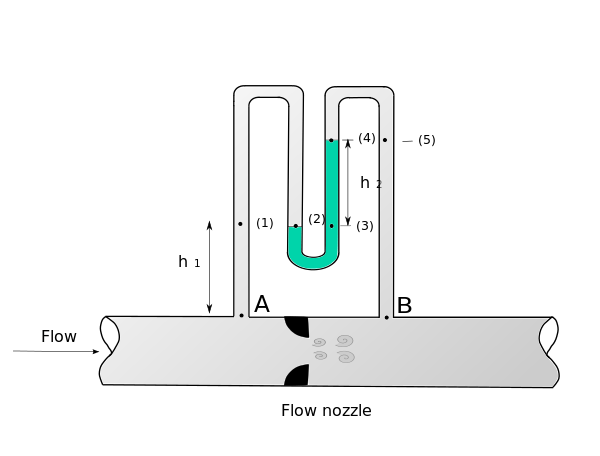 Application of U tube manometer to measure pressure difference |
Inclined-Tube Manometer
|
To measure small pressure changes, a monometer of the type shown in the figure, is frequently used. One leg of the manometer is inclined at an angle 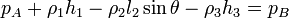 or 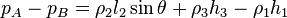 where the pressure difference between points (1) and (2) is due to the vertical distance between the points, which can be expressed as 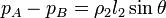
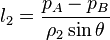 where the contributions of the gas columns |
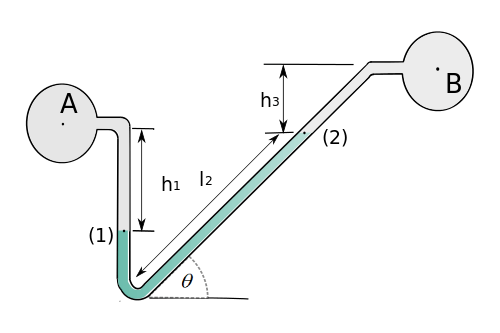 inlclined-Tube manometer to measure small difference |
Other related topics
Buoyancy and calculation of forces on the submerged surfaces are topics related to fluid statics.
![\displaystyle dF_{2}^{pressure} = \left[P-\frac{\partial P}{\partial x_{2}}\frac{dx_{2}}{2}\right]dx_{1}\ dx_{3} - \left[P + \frac{\partial P}{\partial x_{2}}\frac{dx_{2}}{2}\right]dx_{1}\ dx_{3}](../I/m/abdd58462161f25d839f74c7a77b7198.png)
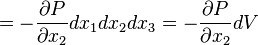
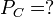
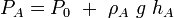
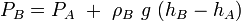
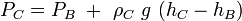
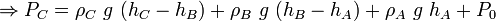
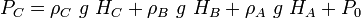
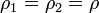
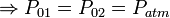
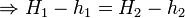
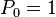 atm =
atm = 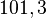 kPa
kPa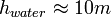 where as height of mercury will be around
where as height of mercury will be around 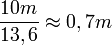 So now taking this barometer to desired location and observing the mercury column height, the atmospheric pressure could be
measured.
So now taking this barometer to desired location and observing the mercury column height, the atmospheric pressure could be
measured.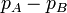 , along the pipe which is related to the flow through the equation
, along the pipe which is related to the flow through the equation 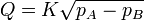 where K is a constant depending on the pipe and nozzle size. The pressure drop is frequently measured with a differential U-tube manometer of the type illustrated. (a) Determine an equation for
where K is a constant depending on the pipe and nozzle size. The pressure drop is frequently measured with a differential U-tube manometer of the type illustrated. (a) Determine an equation for 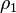 , the specific weight of the gage fluid,
, the specific weight of the gage fluid, 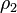 , and the various heights indicated. (b) For
, and the various heights indicated. (b) For 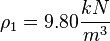 ,
, 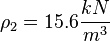 ,
, 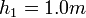 and
and 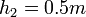 , what is the value of the pressure drop,
, what is the value of the pressure drop, 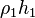 and will be equal to the pressure at (2) and (3). We can move from (3) to (4) where the pressure has been further reduced by
and will be equal to the pressure at (2) and (3). We can move from (3) to (4) where the pressure has been further reduced by 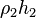 . The pressures at levels (4) and (5) are equal, and as we move from (5) to B the pressure will increase by
. The pressures at levels (4) and (5) are equal, and as we move from (5) to B the pressure will increase by 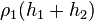 .
.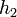 . The diferential manometer could be placed 0.5 m or 5.0 m above the pipe
. The diferential manometer could be placed 0.5 m or 5.0 m above the pipe 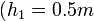 or
or 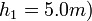 and the value of
and the value of 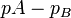 ,if the difference between
,if the difference between 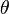 , and the differential reading
, and the differential reading 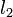 is measured along the inclined tube. The difference in pressure
is measured along the inclined tube. The difference in pressure 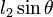 . Thus, for relatively small angles the differential reading along the inclined tube can be made large even for small pressure differences. The inclined-tube manometer is often used to measure small differences in gas pressures so that if pipes A and B contain a gas then
. Thus, for relatively small angles the differential reading along the inclined tube can be made large even for small pressure differences. The inclined-tube manometer is often used to measure small differences in gas pressures so that if pipes A and B contain a gas then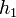 and
and 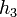 have been neglected. The equation above shows that the differential reading
have been neglected. The equation above shows that the differential reading 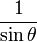 . Recall that
. Recall that 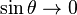 as
as 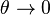 .
.