Floating point/Introduction

What Floating Point Is

Floating point is a way to represent numbers and do arithmetic in computing machines, ranging from simple calculators to computers.

Take the number π. In order for us to accurately represent the area of a circle with radius 3, we have to notate the area as 9π. We can easily compare 9π to other numbers, such as 27, 400, or ². A computer can't. In order for the computer to compare 9π to these numbers, it first has to compute 9π, and store this number. In order for this number to be accurate, it has to have an infinite storage space. This would imply a huge cost (infinite), and little would be gained. Instead, the computer rounds 9π to some arbitrary place, and this uses this stored number in calculations.

If the stored number has enough accuracy, then we're fine. But sometimes there are problems. If all numbers are stored in three decimal digits, then 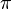is stored as 3.14. 9 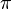would be computed as 9 × 3.14 = 28.26 ~ 28.3. If we continue to have to use this number, and we repeat this process, eventually, our number will continue to become inaccurate.

Who This Course is For

This course is for those interested in computer science and mathematics. Additionally, anyone using computers for numerical purposes can benefit in knowing what can go wrong in a computation.

Why This is Important

Numerical errors vis-a-vis computing devices have cost the world billions of dollars and have cost lives. This may be very surprising, given at first glance, these problems seem very simple. However, because of their simplicity, these issues are often overlooked.

• In 1995, Intel created a public relations nightmare when their new line of processors did not compute certain divisions accurately. After eight months of bickering with the public, Intel had to ship fixes for their processors. This is the most widely cited example of a numerical problem, and it cost the company $480 million.^[1]
• In the First Gulf War, a numerical error cost the lives of 28 American soldiers stationed in Saudi Arabia. A machine designed to intercept missiles propagated an error over time and needed to be rebooted every 20 hours. After 100 hours, it failed to intercept a missile, and people were killed.^[2]
• The European Space Agency lost $500 million when a rocket exploded 40 seconds after it was launched in French Guiana. The error was due to an error in converting a floating number to an integer; the range of integers in the machine only amounted to 32767, much less than what was needed in the conversion.^[3]

Homework

Find another example of a costly floating point error on the internet. What was the problem? How much did it cost?

References