Factorising quadratics
| |
Educational level: this is a secondary education resource. |
Quadratic equations are equations of the form 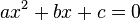 where a, b and c are constants,
where a, b and c are constants, 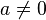 and
and  is a variable. In other words, a quadratic equation has at least one term of the variable, say
is a variable. In other words, a quadratic equation has at least one term of the variable, say  , raised to the exponent
, raised to the exponent 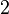 , e.g.
, e.g. 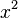
| |
Subject classification: this is a mathematics resource . |
Arranging terms
Arrange the quadratic into order: first the squared number ax2, then the number times x, bx, finally the constant value c.
Factorising quadratics
Form of quadratics: 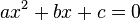
To factorise:
- split the middle term so it adds to the original number, e.g., let b = (AD + BC), and
- multiplies to the constant times the first term, e.g., Ax times Bx equals ABx2, then a = AB,
- then bracket so the pronumeral (letter) is like this, e.g., (Ax + C)(Bx + D).
Checking
Multiplying the two terms: 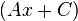 and
and 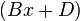 with each other becomes:
with each other becomes:
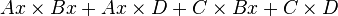
which rearranges to:
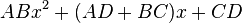
The final constant 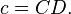
Examples
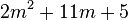
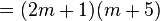
To check it, re-expand the answer to see if we get back to where we started from:
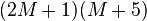
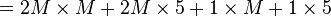
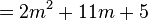
See also
References
External links
This article is issued from Wikiversity - version of the Tuesday, February 09, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.