Exercises on the bisection method

Exercises on the bisection method

Numerical analysis > Exercises on the bisection method

Exercise 1

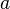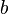Write a Octave/MATLAB function for the bisection method. The function takes as arguments the function $f$ , the extrema of the interval $a$ and $b$ , the tolerance $\epsilon$ and the maximum number of iterations.
Consider the function 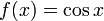in .
1. How many roots are there in this interval?
2. Theoretically, how many iterations are needed to find a solution?
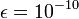3. With $\epsilon=10^{-10}$ , how many iterations are needed? Does the numerical result satisfy this condition?
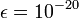4. With $\epsilon=10^{-20}$ , how many iterations are needed? Does the numerical result satisfy this condition?

Exercise 2

Consider the function 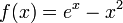in .
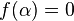1. Show the existence and uniqueness of the root $f(\alpha)=0$ .
2. Given the tolerance 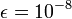$\epsilon=10^{-8}$ , how many iterations are needed?
3. Consideri the restriction of the interval to $\displaystyle [-2, -1]$ . In this case how many iterations are needed?
4. With the aid pf the Octave/MATLAB function of exercise 1, compute the root of the function.
5. Compute the solution with precision 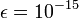$\epsilon=10^{-15}$ e consider it as the exact solution. Then considering 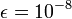$\epsilon=10^{-8}$ , draw a logarithmic plot to represent the average error and the actual error. Comment.

Exercise 3

Show that the sequence defined by the bisection method with 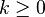$k\geq 0$ we have

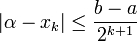|\alpha-x_k|\leq \frac{b-a}{2^{k+1}}

This article is issued from Wikiversity - version of the Sunday, March 06, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.