Exact differential equations
| | Educational level: this is a tertiary (university) resource. |
| | Resource type: this resource is a lesson. |
| | Subject classification: this is a mathematics resource . |
| | Completion status: this resource is ~25% complete. |
School:Mathematics > Topic:Differential_Equations > Ordinary Differential Equations > Exact Differential Equations
Definition
A differential equation of is said to be exact if it can be written in the form 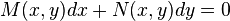 where
where 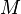 and
and 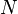 have continuous partial derivatives such that
have continuous partial derivatives such that 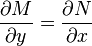 .
.
Solution
Solving the differential equation consists of the following steps:
- Create a function
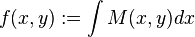 . While integrating, add a constant function
. While integrating, add a constant function 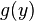 that is a function of
that is a function of 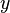 . This is a term that becomes zero if function
. This is a term that becomes zero if function 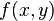 is differentiated with respect to
is differentiated with respect to  .
. - Differentiate the function
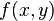 with respect to
with respect to 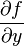 . Set
. Set 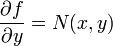 . Solve for the function
. Solve for the function 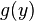 .
.
This article is issued from Wikiversity - version of the Saturday, July 09, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.