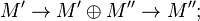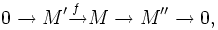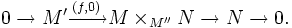Exact additive category
Exact additive category is a category which is both additive and exact.
- 1. An additive category definition can be found in the attached reference[1]
- 2. Exact categories properties are related to those of abelian categories in the following way. assume
 to be an abelian category and let
to be an abelian category and let  be any strictly full additive subcategory which is closed under taking extensions in the sense that given an exact sequence
be any strictly full additive subcategory which is closed under taking extensions in the sense that given an exact sequence
in 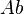 , and then if
, and then if 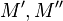 are in
are in  , so is
, so is 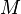 . We can take the class
. We can take the class  to be simply the sequences in
to be simply the sequences in  which are exact in
which are exact in 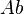 ; that is,
; that is,
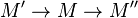 is in
is in  iff
iff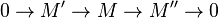
is exact in  . Then
. Then  is an exact category in the following sense.
is an exact category in the following sense.
- 3. An exact category,
 , is an additive category possessing a class Es of "short exact sequences", that is, triples of objects connected by arrows
, is an additive category possessing a class Es of "short exact sequences", that is, triples of objects connected by arrows
satisfying the following axioms that are related to the properties of short exact sequences of an abelian category:
 is closed under isomorphisms and contains the canonical ("split exact") sequences:
is closed under isomorphisms and contains the canonical ("split exact") sequences:
- Admissible epimorphisms (respectively, admissible monomorphisms) are stable under pullbacks (resp. pushouts): given an exact sequence of objects in
 ,
,
- Admissible epimorphisms (respectively, admissible monomorphisms) are stable under pullbacks (resp. pushouts): given an exact sequence of objects in
- and a map
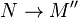 with
with 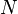 in
in  , one verifies that the following sequence is also exact; since
, one verifies that the following sequence is also exact; since  is stable under extensions, this means that
is stable under extensions, this means that 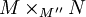 is in
is in  :
:
- Every admissible monomorphism is the kernel of its corresponding admissible epimorphism, and vice-versa: this is true as morphisms in A, and E is a full subcategory.
- If
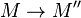 admits a kernel in E and if
admits a kernel in E and if 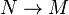 is such that
is such that 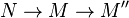 is an admissible epimorphism, then so is
is an admissible epimorphism, then so is 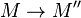 : See Quillen (1972).
: See Quillen (1972).
Note
Conversely, if  is any exact category, we can take
is any exact category, we can take 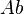 to be the category of left-exact functors from
to be the category of left-exact functors from  into the category of abelian groups, which is itself abelian and in which
into the category of abelian groups, which is itself abelian and in which  is a natural subcategory (via the Yoneda embedding, since Hom is left exact), stable under extensions, and in which a sequence is in Es if and only if it is exact in
is a natural subcategory (via the Yoneda embedding, since Hom is left exact), stable under extensions, and in which a sequence is in Es if and only if it is exact in 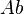 .
.  is any exact category, we can take
is any exact category, we can take 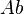 to be the category of left-exact functors from
to be the category of left-exact functors from  into the category of abelian groups, which is itself abelian and in which
into the category of abelian groups, which is itself abelian and in which  is a natural subcategory (via the Yoneda embedding, since the Hom functor is left exact), stable under extensions, and in which a sequence is in Es if and only if it is exact in
is a natural subcategory (via the Yoneda embedding, since the Hom functor is left exact), stable under extensions, and in which a sequence is in Es if and only if it is exact in 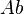 .
.
References
- ↑ http://images.planetmath.org/cache/objects/7922/pdf/AdditiveCategory.pdf Additive Category definition.