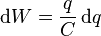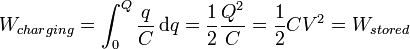Energy stored by a capacitor

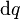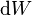The energy (measured in Joules) stored in a capacitor is equal to the work done to charge it. Consider a capacitance C, holding a charge +q on one plate and -q on the other. Moving a small element of charge $\mathrm{d}q$ from one plate to the other against the potential difference V = q/C requires the work $\mathrm{d}W$ :

\mathrm{d}W = \frac{q}{C}\,\mathrm{d}q

where

W is the work measured in joules

q is the charge measured in coulombs

C is the capacitance, measured in farads

We can find the energy stored in a capacitance by integrating this equation. Starting with an uncharged capacitance (q=0) and moving charge from one plate to the other until the plates have charge +Q and -Q requires the work W:

W_{charging} = \int_{0}^{Q} \frac{q}{C} \, \mathrm{d}q = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}CV^2 = W_{stored}

Combining this with the above equation for the capacitance of a flat-plate capacitor, we get:

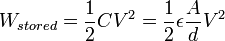W_{stored} = \frac{1}{2} C V^2 = \frac{1}{2} \epsilon \frac{A}{d} V^2

where

W is the energy measured in joules

C is the capacitance, measured in farads

V is the voltage measured in volts

This article is issued from Wikiversity - version of the Friday, November 27, 2009. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.