Electrostatic fields

The electric force acting on a charged object can be interpreted as being produced by some property of the space where that object is located. That property of space that leads to forces over the electrostatic charges is called electric field.

In mathematical terms, the electric field can be defined precisely in the following way: at any point in space the electric field is a vector 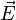$\vec{E}$ obtained by dividing the force 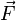$\vec{F}$ acting on a point charge 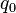$q_0$ placed in that point, over the value of the charge:

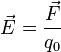
$\vec{E} = \frac{\vec{F}}{q_0}$

The source of the electric field can be either other electrostatic charges, or a varying magnetic field. If the field is produced by electric charges, it is called electrostatic. In that case, it can be shown that is is a conservative field; namely, the path integral of the field between two points is independent of the path. As a consequence, it is possible to define a potential function: the potential in any point of space 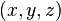$(x,y,z)$ is equal to the path integral of the electrostatic field from an arbitrary reference point 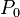$P_0$ until the point $(x,y,z)$ .

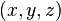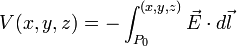
$V(x,y,z) = -\int_{P_0}^{(x,y,z)} \vec{E}\cdot d\vec{l}$

Thus, the electrostatic potential (also known as voltage) is a scalar field and it can be proved that the gradient of that scalar field is equal to minus the electrostatic field:

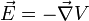
$\vec{E} = -\vec{\nabla} V$

Surfaces, each point of which has equal potential (φ = Const), are called equipotential.

This article is issued from Wikiversity - version of the Monday, February 08, 2010. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.