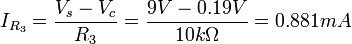|
Exercise 7: Answers
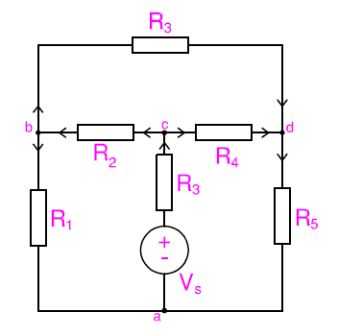
KCL @ Node b:
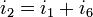
Thus by applying Ohms law to above equation we get.
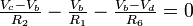
Therefore
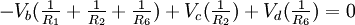 ............... (1) ............... (1)
KCL @ Node c:
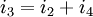
Thus by applying Ohms law to above equation we get.
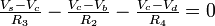
Therefore
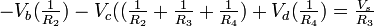 ............... (2) ............... (2)
KCL @ Node d:
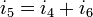
Thus by applying Ohms law to above equation we get.
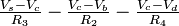
Therefore
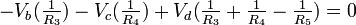 ............... (3) ............... (3)
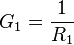 etc thus equations 1; 2 & 3 will be re-written as follows: etc thus equations 1; 2 & 3 will be re-written as follows:
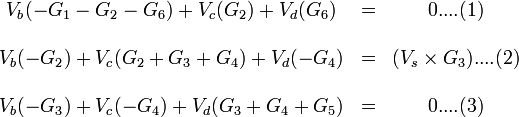
Now we can create a matrix with the above equations as follows:
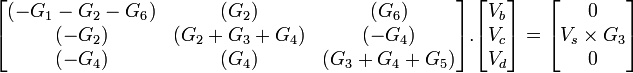
The following matrix is the above with values substituted:
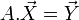 → → 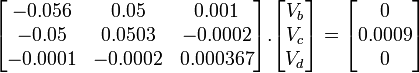
Now that we have arranged equations 1; 2 & 3 into a matrix we need to get Determinants of the General matrix, and Determinants of alterations of the general matrix as follows:
Solving determinants of:
- Matrix A : General matrix A from KCL equations
- Matrix A1 : Genral Matrix A with Column 1 substituted by
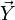 . .
- Matrix A2 : Genral Matrix A with Column 2 substituted by
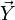 . .
- Matrix A3 : Genral Matrix A with Column 3 substituted by
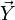 . .
As follows:
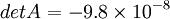
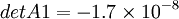
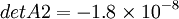
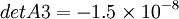
Now we can use the solved determinants to arrive at solutions for Node voltages 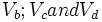 as follows: as follows:
1. 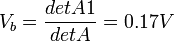
2. 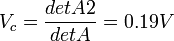
3. 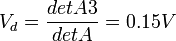
Now we can apply Ohm's law to solve for the current through 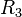 as follows: as follows:
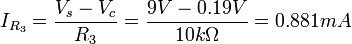
| 
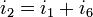
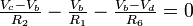
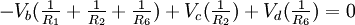 ............... (1)
............... (1)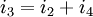
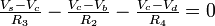
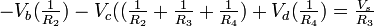 ............... (2)
............... (2)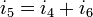
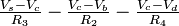
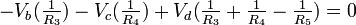 ............... (3)
............... (3)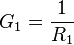 etc thus equations 1; 2 & 3 will be re-written as follows:
etc thus equations 1; 2 & 3 will be re-written as follows: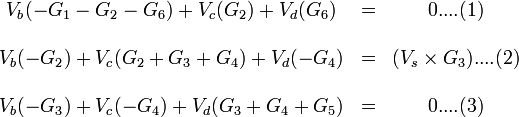
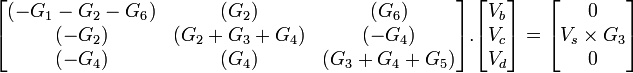
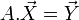 →
→ 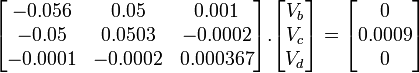
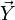 .
.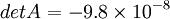
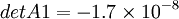
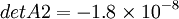
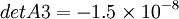
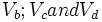 as follows:
as follows: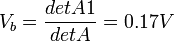
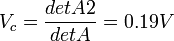
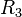 as follows:
as follows: