Electric Circuit Analysis/Mesh Analysis/Answers
< Electric Circuit Analysis < Mesh Analysis|
Exercise 8: Answers
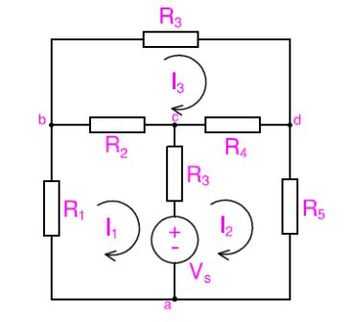
KVL arround abca loop: Therefore
Therefore
Therefore
Now we can create a matrix with the above equations as follows: The following matrix is the above with values substituted:
Solving determinants of:
As follows:
2. 3. Now we can solve for the current through The negative sign means that |
This article is issued from Wikiversity - version of the Saturday, January 18, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
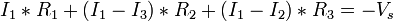
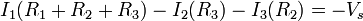 ............... (1)
............... (1)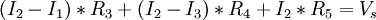
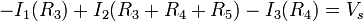 ............... (2)
............... (2)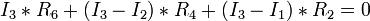
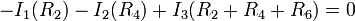 ............... (3)
............... (3)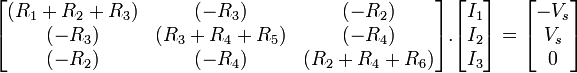
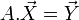 →
→ 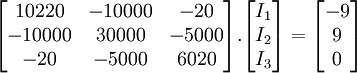
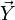 .
.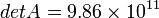
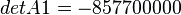
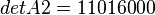
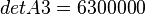
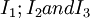 as follows:
as follows: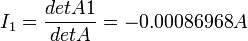
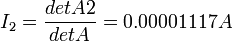
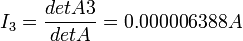
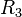 as follows:
as follows: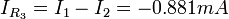
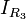 is flowing in the direction of
is flowing in the direction of 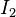 .
.