Electric Circuit Analysis/Kirchhoff's Current Law/Answers
< Electric Circuit Analysis < Kirchhoff's Current Law|
Exercise 6: Answers
From The Diagram From Node b we get: From Node d we get: It is clear that we must solve V_c, in order to complete Voltage definitions at all nodes. V_c will be found by applying KCL at Node c and solving resulting equations Follows:
We can group like terms to get the following equation: Substitute values into previous equations you get:
Thus now we can calculate Current through Thus the effective current through |
This article is issued from Wikiversity - version of the Saturday, January 18, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
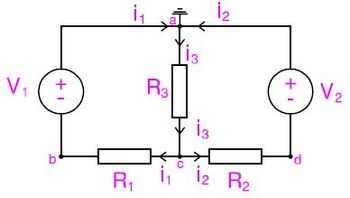
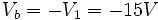
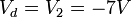
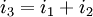
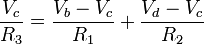
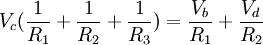
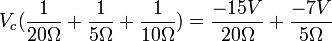
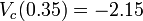 thus
thus 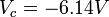
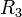 as follows:
as follows:
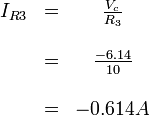 .
. Just as we expected!
Just as we expected!