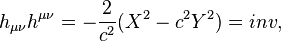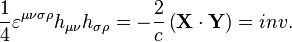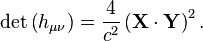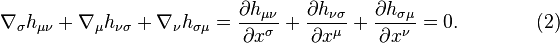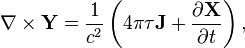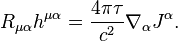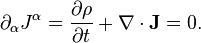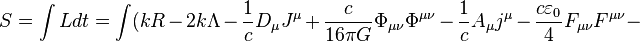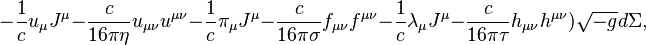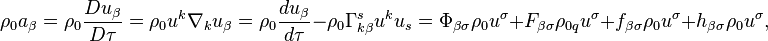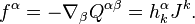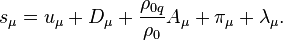Dissipation field tensor
The dissipation field tensor is an antisymmetric tensor describing the energy dissipation due to viscosity and consisting of six components. Tensor components are at the same time components of the two three-dimensional vectors – dissipation field strength and the solenoidal dissipation vector. With the dissipation field tensor the dissipation stress-energy tensor, the dissipation field equations and dissipation force in matter are defined. Dissipation field is a component of general field.
Definition
Expression for the dissipation field tensor can be found in papers by Sergey Fedosin, [1] where the tensor is defined using 4-curl:
Here dissipation 4-potential 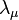 is given by:
is given by:
where  is the scalar potential,
is the scalar potential,
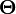 is the vector potential of dissipation field,
is the vector potential of dissipation field,
 – speed of light.
– speed of light.
Expression for the components
The dissipation field strength and the solenoidal dissipation vector are found with the help of (1):
and the same in vector notation:
The dissipation field tensor consists of the components of these vectors:
The transition to the dissipation field tensor with contravariant indices is carried out by multiplying by double metric tensor:
In the special relativity, this tensor has the form:
To convert the components of the dissipation field tensor from one inertial system to another we must take into account the transformation rule for tensors. If the reference frame K' moves with an arbitrary constant velocity 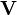 with respect to the fixed reference system K, and the axes of the coordinate systems are parallel to each other, the dissipation field strength and the solenoidal dissipation vector are converted as follows:
with respect to the fixed reference system K, and the axes of the coordinate systems are parallel to each other, the dissipation field strength and the solenoidal dissipation vector are converted as follows:
Properties of tensor
-
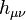 is the antisymmetric tensor of rank 2, from this the condition follows
is the antisymmetric tensor of rank 2, from this the condition follows 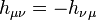 . Three of the six independent components of the dissipation field tensor are associated with the components of the dissipation field strength
. Three of the six independent components of the dissipation field tensor are associated with the components of the dissipation field strength  , and the other three – with the components of the solenoidal dissipation vector
, and the other three – with the components of the solenoidal dissipation vector  . Due to the antisymmetry such invariant as the contraction of the tensor with the metric tensor vanishes:
. Due to the antisymmetry such invariant as the contraction of the tensor with the metric tensor vanishes: 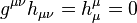 .
. - Contraction of tensor with itself
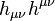 is an invariant, and the contraction of tensor product with Levi-Civita symbol as
is an invariant, and the contraction of tensor product with Levi-Civita symbol as 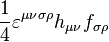 is the pseudoscalar invariant. These invariants in the special relativity can be expressed as follows:
is the pseudoscalar invariant. These invariants in the special relativity can be expressed as follows:
- Determinant of the tensor is also Lorentz invariant:
Dissipation field
Through the dissipation field tensor the equations of dissipation field are written:
where 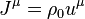 is the mass 4-current,
is the mass 4-current, 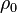 is the mass density in comoving reference frame,
is the mass density in comoving reference frame, 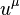 is the 4-velocity,
is the 4-velocity, 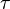 is a constant.
is a constant.
Instead of (2) it is possible to use the expression:
Equation (2) is satisfied identically, which is proved by substituting into it the definition for the dissipation field tensor according to (1). If in (2) we insert tensor components 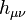 , this leads to two vector equations:
, this leads to two vector equations:
According to (5), the solenoidal dissipation vector has no sources as its divergence vanishes. From (4) it follows that the time variation of the solenoidal dissipation vector leads to a curl of the dissipation field strength.
Equation (3) relates the dissipation field to its source in the form of mass 4-current. In Minkowski space of special relativity the form of the equation is simplified and becomes:
где 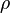 – плотность движущейся массы,
– плотность движущейся массы,
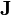 – плотность тока массы.
– плотность тока массы.
According to the first of these equations, the dissipation field strength is generated by the mass density, and according to the second equation the mass current or change in time of the dissipation field strength generate the circular field of the solenoidal dissipation vector.
From (3) and (1) we can obtain continuity equation:
This equation means that due to the curvature of space-time when the Ricci tensor 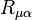 is non-zero, the dissipation field tensor
is non-zero, the dissipation field tensor 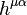 is a possible source of divergence of mass 4-current. If space-time is flat, as in Minkowski space, the left side of the equation is set to zero, the covariant derivative becomes the 4-gradient and remains the following:
is a possible source of divergence of mass 4-current. If space-time is flat, as in Minkowski space, the left side of the equation is set to zero, the covariant derivative becomes the 4-gradient and remains the following:
Covariant theory of gravitation
Action and Lagrangian
Total Lagrangian for the matter in gravitational and electromagnetic fields includes the dissipation field tensor and is contained in the action function: [1]
where 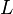 is Lagrangian,
is Lagrangian, 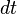 is differential of coordinate time,
is differential of coordinate time, 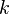 is a certain coefficient,
is a certain coefficient, 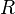 is the scalar curvature,
is the scalar curvature, 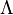 is the cosmological constant, which is a function of the system,
is the cosmological constant, which is a function of the system,  is the speed of light as a measure of the propagation speed of electromagnetic and gravitational interactions,
is the speed of light as a measure of the propagation speed of electromagnetic and gravitational interactions, 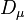 is the gravitational four-potential,
is the gravitational four-potential, 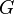 is the gravitational constant,
is the gravitational constant, 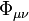 is the gravitational tensor,
is the gravitational tensor, 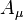 is the electromagnetic 4-potential,
is the electromagnetic 4-potential, 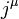 is the electromagnetic (charge) 4-current,
is the electromagnetic (charge) 4-current, 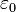 is the vacuum permittivity,
is the vacuum permittivity, 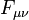 is the electromagnetic tensor,
is the electromagnetic tensor, 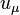 is the covariant 4-velocity,
is the covariant 4-velocity, 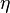 ,
, 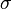 and
and 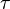 are some constants,
are some constants, 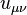 is the acceleration tensor,
is the acceleration tensor, 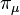 is the 4-potential of pressure field,
is the 4-potential of pressure field, 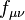 is the pressure field tensor,
is the pressure field tensor, 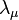 is the 4-potential of dissipation field,
is the 4-potential of dissipation field, 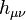 is the dissipation field tensor,
is the dissipation field tensor, 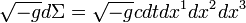 is the invariant 4-volume,
is the invariant 4-volume, 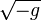 is the square root of the determinant
is the square root of the determinant 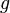 of metric tensor, taken with a negative sign,
of metric tensor, taken with a negative sign, 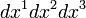 is the product of differentials of the spatial coordinates.
is the product of differentials of the spatial coordinates.
The variation of the action function by 4-coordinates leads to the equation of motion of the matter unit in gravitational and electromagnetic fields, pressure field and dissipation field:
where 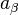 is the 4-acceleration with the covariant index, the operator of proper-time-derivative with respect to proper time
is the 4-acceleration with the covariant index, the operator of proper-time-derivative with respect to proper time 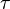 is used, the first term on the right is the gravitational force density, expressed with the help of the gravitational field tensor, second term is the Lorentz electromagnetic force density for the charge density
is used, the first term on the right is the gravitational force density, expressed with the help of the gravitational field tensor, second term is the Lorentz electromagnetic force density for the charge density 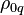 measured in the comoving reference frame, and the two last term set the pressure force density and the dissipation force density, respectively.
measured in the comoving reference frame, and the two last term set the pressure force density and the dissipation force density, respectively.
If we vary the action function by the dissipation 4-potential, we obtain the equation of dissipation field (3).
Dissipation stress-energy tensor
With the help of dissipation field tensor in the covariant theory of gravitation the dissipation stress-energy tensor is constructed:
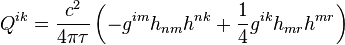 .
.
The covariant derivative of the dissipation stress-energy tensor determines the dissipation four-force density:
Generalized velocity and Hamiltonian
Covariant 4-vector of generalized velocity is given by:
With regard to the generalized 4-velocity, the Hamiltonian contains the dissipation field tensor and has the form:
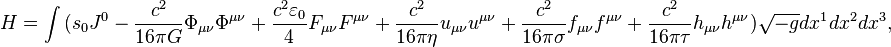
where 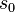 and
and 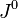 are timelike components of 4-vectors
are timelike components of 4-vectors 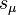 and
and 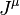 .
.
In the reference frame that is fixed relative to the center of mass of system, the Hamiltonian will determine the invariant energy of the system.
See also
- Electromagnetic tensor
- Gravitational tensor
- Acceleration tensor
- Pressure field tensor
- Dissipation stress-energy tensor
- General field
- Dissipation field
- Acceleration field
- Pressure field
- Lorentz-invariant theory of gravitation
- Covariant theory of gravitation
References
- 1 2 Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18 (No. 1), pp. 13-24, 2015. http://dx.doi.org/10.5541/ijot.5000034003.
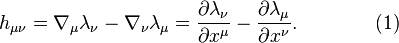
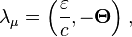
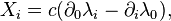
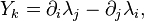
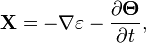

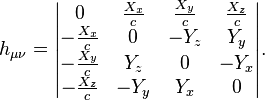
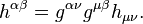
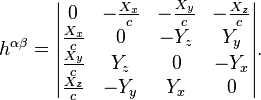
![\mathbf {X}^\prime = \frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {X}) + \frac {1}{\sqrt{1 - {V^2 \over c^2}}} \left(\mathbf {X}-\frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {X}) + [\mathbf {V} \times \mathbf {Y }] \right),](../I/m/1773ec7835de3e55298517d9e709fe30.png)
![\mathbf {Y }^\prime = \frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {Y }) + \frac {1}{\sqrt{1 - {V^2 \over c^2}}} \left(\mathbf {Y }-\frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {Y }) - \frac {1}{ c^2} [\mathbf {V} \times \mathbf {X}] \right).](../I/m/2abaf303b8db9d401348e79768f5ca99.png)