Dirichlet conditions

Dirichlet conditions guarantee that a periodic function 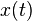$x(t)$ can be exactly represented by its Fourier transform.

Readings

Wikipedia: Dirichlet conditions

Conditions

Condition 1

The function must be absolutely integrable over a single period 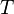$T$ . This is equivalent to the statement that the area enclosed between the abcissa and the function is finite over a single period.

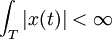
$\int_T|x(t)|<\infty$

Condition 2

Given any finite period of time the number of local maxima and minima of 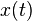$x(t)$ within that period is finite.

Condition 3

Given any finite period of time there is a finite number of discontinuities in the function 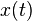$x(t)$

This article is issued from Wikiversity - version of the Monday, April 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.